高三数学 1直线与直线垂直试题-人教版高三全册数学试题VIP专享VIP免费

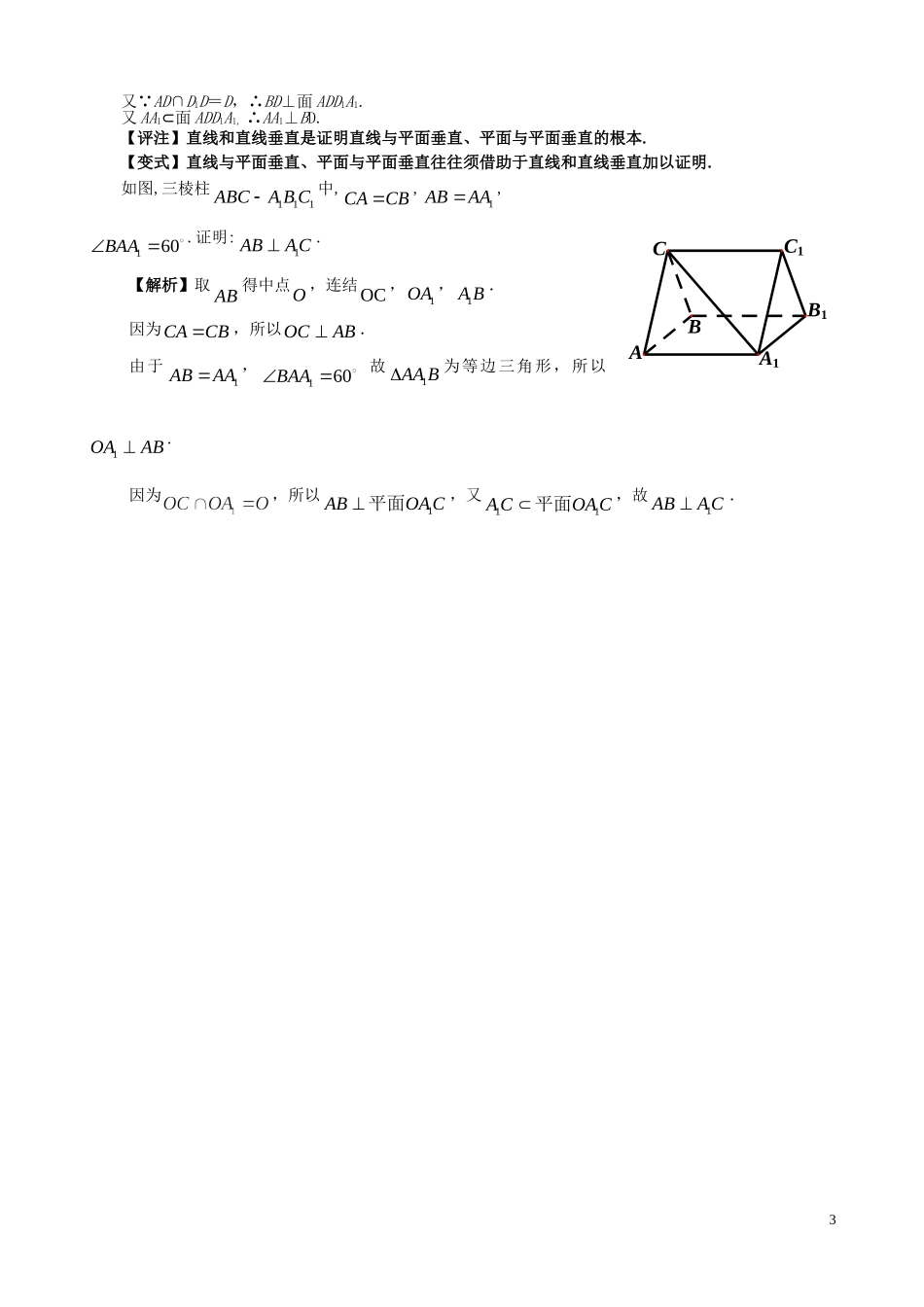
1.直线与直线垂直1.1空间直线的垂直定义【例1】若空间中四条两两不同的直线1l、2l、3l、4l，满足12ll，23//ll，34ll，则下列结论一定正确的是（）A.14llB.14//llC.1l、4l既不平行也不垂直D.1l、4l的位置关系不确定【解析】如图所示，在正方体ABCDA1B1C1D1中，设BB1是直线l1，BC是直线l2，AB是直线l3，则DD1是直线l4，l1∥l4；设BB1是直线l1，BC是直线l2，CC1是直线l3，CD是直线l4，则l1⊥l4.故l1与l4的位置关系不确定．【评注】考查空间中直线的位置关系，合理地构造几何模型进行判断即可．【变式】如果两条直线所成的角为，则这两条直线垂直.如图，在直三棱柱中，，，BC=1，，M是CC1的中点．求证：.【解析】因为三棱柱为直棱柱，故，所以，又，故，则平面．连接，则为在平面内的射影．可得到∽，则，因为，所以，∴．由三垂线定理可得．1.2直线与直线垂直的判定【例2】平面，证明：．【解析】因为，所以；因为，所以，所以平面，又平面，所以．【评注】如果一条直线垂直于一个平面，则这条直线垂直于这个平面内的任意一条直线，其推理模式：．【变式1】三垂线定理：在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直，其推理模式：．1如图，斜边为的，．证明：；【解析】因为，，所以，又，所以.【变式2】三垂线定理的逆定理：在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直，其推理模式：．如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上．【解析】已知：在内，于，于且，求证：在的平分线上（即）．分析：∵，∴（三垂线定理逆定理）；∵，∴，∴，又∵，∴，∴．【变式3】三垂线定理的定理与逆定理的综合应用.点为所在平面外的一点，点为点在平面内的射影，若，求证：．【解析】连结，，且，∴（三垂线定理逆定理）；同理，∴为的垂心，∴，又，∴（三垂线定理）．1.3直线与直线垂直的性质【例3】如图，在四棱台ABCDA1B1C1D1中，D1D⊥平面ABCD，底面ABCD是平行四边形，AB＝2AD，AD＝A1B1，∠BAD＝60°.证明：.【解析】∵D1D⊥面ABCD，且BD⊂面ABCD，∴D1D⊥BD.又∵AB＝2AD，∠BAD＝60°，在△ABD中，由余弦定理得BD2＝AD2＋AB2－2AD·ABcos60°＝3AD2，∴AD2＋BD2＝AB2.即AD⊥BD.2又∵AD∩D1D＝D，∴BD⊥面ADD1A1.又AA1⊂面ADD1A1,∴AA1⊥BD.【评注】直线和直线垂直是证明直线与平面垂直、平面与平面垂直的根本.【变式】直线与平面垂直、平面与平面垂直往往须借助于直线和直线垂直加以证明.如图,三棱柱111ABCABC中,CACB,1ABAA,160BAA.证明:1ABAC.【解析】取AB得中点O，连结OC，1OA，1AB．因为CACB，所以OCAB．由于1AAAB，601BAA故1AAB为等边三角形，所以1OAAB.因为，所以1ABOAC平面，又COACA11平面，故1ABAC．3C1B1AA1BC