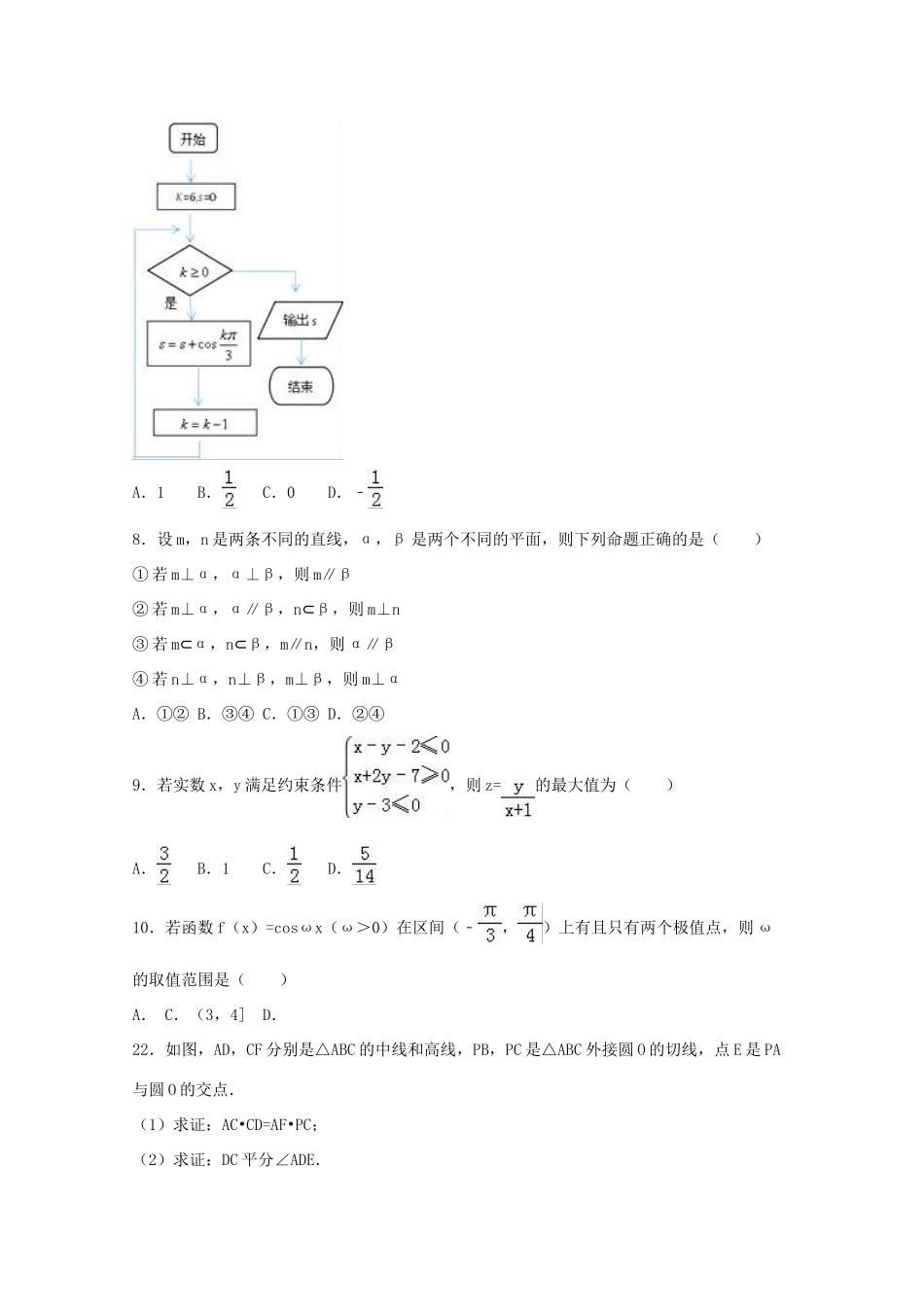
2016年福建省厦门市高考数学二模试卷(文科)一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={﹣2,﹣1,0,1,2},B={x|2x>1},则A∩B=()A.{﹣1,2}B.{0,1}C.{1,2}D.{0,1,2}2.幂函数y=f(x)的图象经过点(2,4),则f(x)的解析式为()A.f(x)=2xB.f(x)=x2C.f(x)=2xD.f(x)=log2x+33.一个口袋中装有大小和形状完全相同的2个红球和2个白球,从这个口袋中任取2个球,则取得的两个球中恰有一个红球的概率是()A.B.C.D.4.双曲线﹣=1(a>0,b>0)的实轴为A1A2,虚轴的一个端点为B,若三角形A1A2B的面积为b2,则双曲线的离心率()A.B.C.D.5.若2sin2α=1﹣cos2α,则tanα等于()A.﹣2B.2C.﹣2或0D.2或06.已知向量=(1,m),=(3,),若向量,的夹角为,则实数m的值为()A.﹣B.﹣C.D.7.执行如图所示的程序框图,则输出s的值等于()A.1B.C.0D.﹣8.设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是()①若m⊥α,α⊥β,则m∥β②若m⊥α,α∥β,n⊂β,则m⊥n③若m⊂α,n⊂β,m∥n,则α∥β④若n⊥α,n⊥β,m⊥β,则m⊥αA.①②B.③④C.①③D.②④9.若实数x,y满足约束条件,则z=的最大值为()A.B.1C.D.10.若函数f(x)=cosωx(ω>0)在区间(﹣,)上有且只有两个极值点,则ω的取值范围是()A.C.(3,4]D.22.如图,AD,CF分别是△ABC的中线和高线,PB,PC是△ABC外接圆O的切线,点E是PA与圆O的交点.(1)求证:AC•CD=AF•PC;(2)求证:DC平分∠ADE.23.在平面直角坐标系xOy中,曲线C的方程为x2﹣2x+y2=0,以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为θ=(ρ∈R).(Ⅰ)写出C的极坐标方程,并求l与C的交点M,N的极坐标;(Ⅱ)设P是椭圆+y2=1上的动点,求△PMN面积的最大值.24.已知函数f(x)=|x﹣3|.(1)求不等式f(x)<2+|x+1|的解集;(2)已知m,n∈R+且+=2mn,求证:mf(n)+nf(﹣m)≥6.2016年福建省厦门市高考数学二模试卷(文科)参考答案与试题解析一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={﹣2,﹣1,0,1,2},B={x|2x>1},则A∩B=()A.{﹣1,2}B.{0,1}C.{1,2}D.{0,1,2}【考点】交集及其运算.【分析】求出B中不等式的解集确定出B,找出A与B的交集即可.【解答】解:由B中不等式变形得:2x>1=20,即x>0,∴B=(0,+∞),又 A={﹣2,﹣1,0,1,2},∴A∩B={1,2},故选:C.2.幂函数y=f(x)的图象经过点(2,4),则f(x)的解析式为()A.f(x)=2xB.f(x)=x2C.f(x)=2xD.f(x)=log2x+3【考点】幂函数的概念、解析式、定义域、值域.【分析】设出幂函数的解析式,利用待定系数法求出解析式即可.【解答】解:设幂函数为f(x)=xa,且y=f(x)的图象经过点(2,4),可得4=2a,解得a=2,∴幂函数的解析式为f(x)=x2.故选:B.3.一个口袋中装有大小和形状完全相同的2个红球和2个白球,从这个口袋中任取2个球,则取得的两个球中恰有一个红球的概率是()A.B.C.D.【考点】列举法计算基本事件数及事件发生的概率.【分析】先求出基本事件总数,再求出取得的两个球中恰有一个红球包含的基本事件个数,由此能求出取得的两个球中恰有一个红球的概率.【解答】解:一个口袋中装有大小和形状完全相同的2个红球和2个白球,从这个口袋中任取2个球,基本事件总数n==6,取得的两个球中恰有一个红球包含的基本事件个数m==4,∴取得的两个球中恰有一个红球的概率p==.故选:D.4.双曲线﹣=1(a>0,b>0)的实轴为A1A2,虚轴的一个端点为B,若三角形A1A2B的面积为b2,则双曲线的离心率()A.B.C.D.【考点】双曲线的简单性质.【分析】根据三角形的面积建立方程关系,建立a,b,c的关系进行求解即可得到结论.【解答】解:设B(0,B),则|A1A2|=2a, 三角形A1A2B的面积为b2,∴S==ab=b2,即a=b,则离心率e====,故选:B.5.若2sin2α=1﹣cos2α,则tanα...