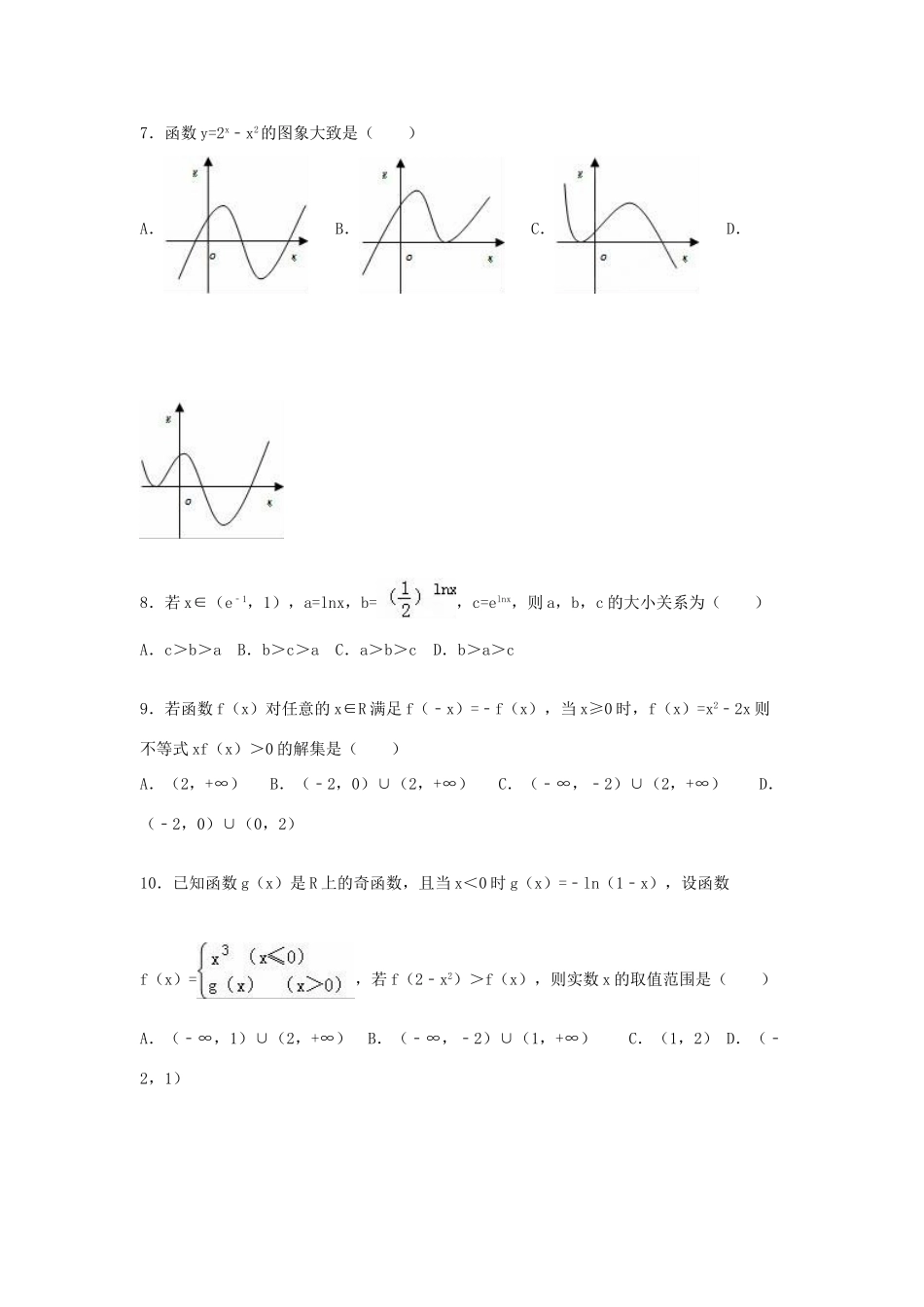
2015-2016学年甘肃省天水市蓓蕾复读部高三(上)第一次月考数学试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|﹣5≤2x﹣1≤3,x∈R},B={x|x(x﹣8)≤0,x∈Z},则A∩B=()A.(0,2)B.[0,2]C.{0,2}D.{0,1,2}2.命题“∀x∈R,ex﹣x+1≥0”的否定是()A.∀x∈R,lnx+x+1<0B.∃x∈R,ex﹣x+1≥0C.∀x∈R,ex﹣x+1>0D.∃x∈R,ex﹣x+1<03.若a,b∈R,则成立的一个充分不必要条件是()A.ab>0B.b>aC.a<b<0D.ab(a﹣b)<04.函数在其定义域内是()A.是增函数又是偶函数B.是增函数又是奇函数C.是减函数又是偶函数D.是减函数又是奇函数5.已知函数f(x)=x3+2x+sinx(x∈R),f(x1)+f(x2)>0,则下列不等式正确的是()A.x1>x2B.x1<x2C.x1+x2<0D.x1+x2>06.设f(x)是定义在R上以2为周期的偶函数,已知x∈(0,1)时,f(x)=(1﹣x),则函数f(x)在(1,2)上()A.是减函数,且f(x)>0B.是增函数,且f(x)>0C.是增函数,且f(x)<0D.是减函数,且f(x)<07.函数y=2x﹣x2的图象大致是()A.B.C.D.8.若x∈(e﹣1,1),a=lnx,b=,c=elnx,则a,b,c的大小关系为()A.c>b>aB.b>c>aC.a>b>cD.b>a>c9.若函数f(x)对任意的x∈R满足f(﹣x)=﹣f(x),当x≥0时,f(x)=x2﹣2x则不等式xf(x)>0的解集是()A.(2,+∞)B.(﹣2,0)∪(2,+∞)C.(﹣∞,﹣2)∪(2,+∞)D.(﹣2,0)∪(0,2)10.已知函数g(x)是R上的奇函数,且当x<0时g(x)=﹣ln(1﹣x),设函数f(x)=,若f(2﹣x2)>f(x),则实数x的取值范围是()A.(﹣∞,1)∪(2,+∞)B.(﹣∞,﹣2)∪(1,+∞)C.(1,2)D.(﹣2,1)11.对于任意的实数a、b,记max{a,b}=.若F(x)=max{f(x),g(x)}(x∈R),其中函数y=f(x)(x∈R)是奇函数,且在x=1处取得极小值﹣2,函数y=g(x)(x∈R)是正比例函数,其图象与x≥0时的函数y=f(x)的图象如图所示,则下列关于函数y=F(x)的说法中,正确的是()A.y=F(x)为奇函数B.y=F(x)有极大值F(﹣1)C.y=F(x)的最小值为﹣2,最大值为2D.y=F(x)在(﹣3,0)上为增函数12.已知函数f(x)=,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是()A.(1,10)B.(10,12)C.(5,6)D.(20,24)二、填空题:本大题共4小题,每小题5分,共20分,把答案填写在题中横线上.13.函数f(x)=log2•log(2x)的最小值为.14.设偶函数f(x)对任意x∈R都有f(x)=﹣,且当x∈[﹣3,﹣2]时,f(x)=4x,则f=.15.已知函数f(x+1)是定义在R上的奇函数,若对于任意给定的不等实数x1、x2,不等式(x1﹣x2)[f(x1)﹣f(x2)]<0恒成立,则不等式f(1﹣x)<0的解集为.16.设α=cos420°,函数f(x)=,则f()+f(log2)的值等于.三.解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.)17.已知关于x的不等式的解集是M.(1)当a=1时,求集合M.(2)当3∈M且5∉M时,求实数a的取值范围.18.已知函数f(x)=x3﹣x2﹣10x,且集合A={x|f′(x)≤0},集合B={x|p+1≤x≤2p﹣1}.若A∪B=A,求p的取值范围.19.已知函数f(x)=log2(|x+1|+|x﹣2|﹣a).(1)当a=4时,求函数f(x)的定义域;(2)若关于x的不等式f(x)≤1的解集不是空集,求a的取值范围.20.求函数y=x2﹣2ax﹣a2﹣1在[0,2]上的最小值g(a)和最大值M(a).21.设函数f(x)=(x﹣1)ex﹣kx2.(1)当k=1时,求函数f(x)的单调区间;(2)若f(x)在x∈[0,+∞)上是增函数,求实数k的取值范围.22.对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知f(x)=ax2+(b+1)x+b﹣1(a≠0).(1)当a=1,b=﹣2时,求函数f(x)的不动点;(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的范围;(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动点,且A、B两点关于直线y=kx+对称,求b的最小值.2015-2...