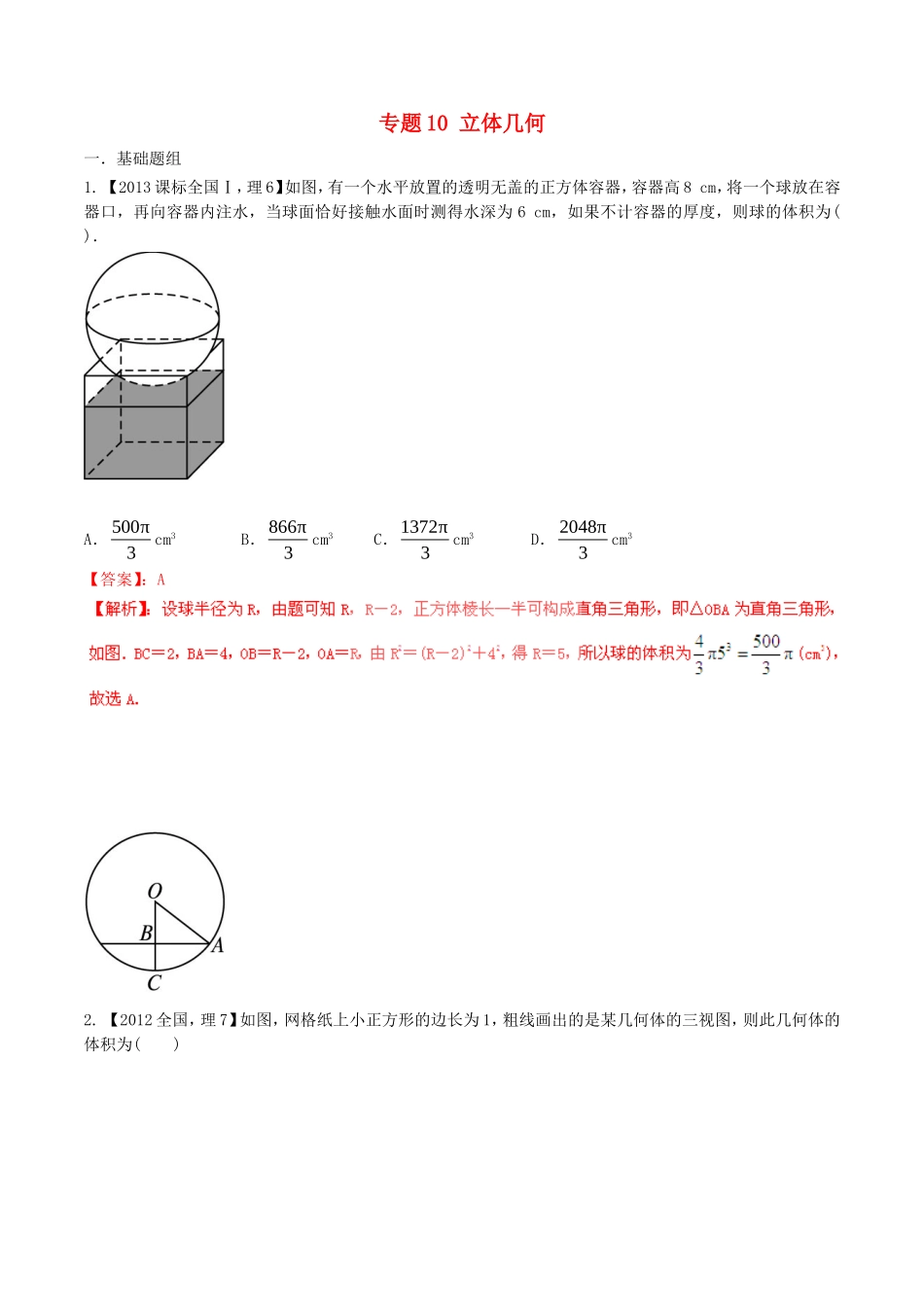
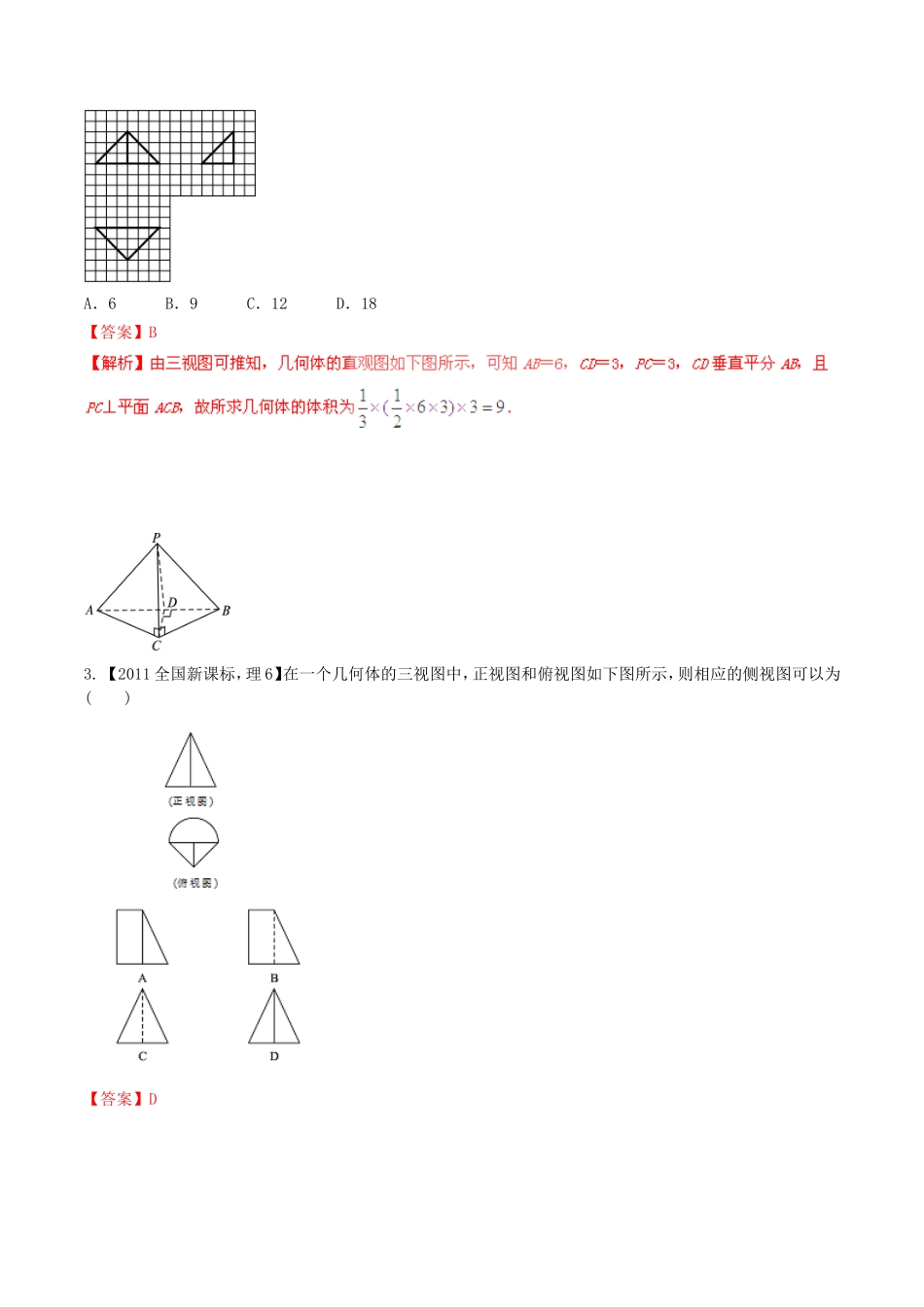
专题10立体几何一.基础题组1.【2013课标全国Ⅰ,理6】如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为().A.500π3cm3B.866π3cm3C.1372π3cm3D.2048π3cm3【答案】:A2.【2012全国,理7】如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A.6B.9C.12D.18【答案】B3.【2011全国新课标,理6】在一个几何体的三视图中,正视图和俯视图如下图所示,则相应的侧视图可以为()【答案】D4.【2006全国,理7】已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是()(A)16π(B)20π(C)24π(D)32π【答案】C5.【2005全国1,理2】一个与球心距离为1的平面截球所得的圆面面积为,则球的表面积为()A.82B.8C.42D.4【答案】B6.【2005全国1,理4】如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE、△BCF均为正三角形,EF//AB,EF=2,则该多面体的体积为()A.32B.33C.34D.23【答案】A7.【2010新课标,理14】正视图为一个三角形的几何体可以是__________.(写出三种)答案:三棱锥、圆锥、四棱锥(答案不唯一)8.【2014课标Ⅰ,理19】(本小题满分12分)如图,三棱柱111CBAABC中,侧面CCBB11为菱形,CBAB1.(Ⅰ)证明:1ABAC;(Ⅱ)若1ACAB,601CBB,BCAB,求二面角111CBAA的余弦值.AA1BB1CC1【答案】(Ⅰ)详见解析;(Ⅱ)17zyOAA1BB1CC19.【2013课标全国Ⅰ,理18】如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.(1)证明:AB⊥A1C;(2)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.10.【2008全国1,理18】(本小题满分12分)四棱锥ABCDE中,底面BCDE为矩形,侧面ABC底面BCDE,2BC,2CD,ABAC.(Ⅰ)证明:ADCE;(Ⅱ)设CE与平面ABE所成的角为45,求二面角CADE的大小.11.【2015高考新课标1,理6】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有()(A)14斛(B)22斛(C)36斛(D)66斛【答案】B【考点定位】圆锥的性质与圆锥的体积公式12.【2015高考新课标1,理18】如图,,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.(Ⅰ)证明:平面AEC⊥平面AFC;(Ⅱ)求直线AE与直线CF所成角的余弦值.【答案】(Ⅰ)见解析(Ⅱ)33【考点定位】空间垂直判定与性质;异面直线所成角的计算;空间想象能力,推理论证能力二.能力题组1.【2013课标全国Ⅰ,理8】某几何体的三视图如图所示,则该几何体的体积为().A.16+8πB.8+8πC.16+16πD.8+16π【答案】:A2.【2011全国,理6】已知直二面角α-l-β,点A∈α,AC⊥l,C为垂足,B∈β,BD⊥l,D为垂足,若AB=2,AC=BD=1,则D到平面ABC的距离等于()A.23B.33C.63D.1【答案】:C3.【2010新课标,理10】设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为()A.πa2B.73πa2C.113πa2D.5πa2【答案】:B4.【2009全国卷Ⅰ,理7】已知三棱柱ABC—A1B1C1的侧棱与底面边长都相等,A1在底面ABC上的射影为BC的中点,则异面直线AB与CC1所成的角的余弦值为()A.43B.45C.47D.43【答案】:D5.【2009全国卷Ⅰ,理10】已知二面角α-l-β为60°,动点P、Q分别在面α、β内,P到β的距离为3,Q到α的距离为32,则P、Q两点之间距离的最小值为()A.2B.2C.32D.4【答案】:C6.【2011全国新课标,理15】已知矩形ABCD的顶点都在半径为4的球O的球面上,且AB=6,BC=23,则棱锥OABCD的体积为__________.【答案】837.【2006全国,理13】已知正四棱...