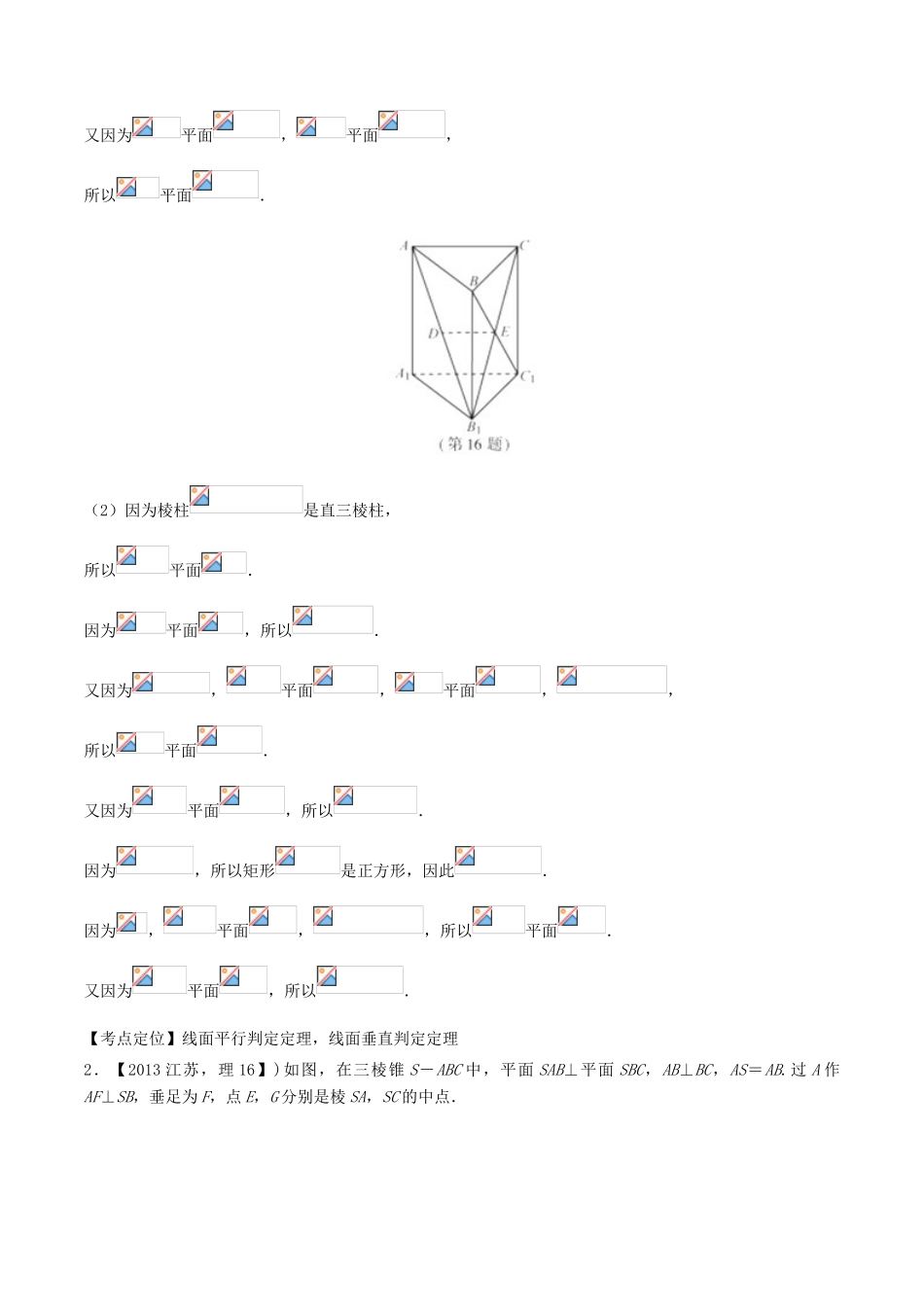
专题2点、直线、平面平行与垂直的判定与性质【三年高考】1.【2015江苏高考,16】如图,在直三棱柱中,已知,,设的中点为,.求证:(1);(2).【答案】(1)详见解析(2)详见解析【解析】试题分析(1)由三棱锥性质知侧面为平行四边形,因此点为的中点,从而由三角形中位线性质得,再由线面平行判定定理得(2)因为直三棱柱中,所以侧面为正方形,因此,又,(可由直三棱柱推导),因此由线面垂直判定定理得,从而,再由线面垂直判定定理得,进而可得试题解析:(1)由题意知,为的中点,又为的中点,因此.又因为平面,平面,所以平面.(2)因为棱柱是直三棱柱,所以平面.因为平面,所以.又因为,平面,平面,,所以平面.又因为平面,所以.因为,所以矩形是正方形,因此.因为,平面,,所以平面.又因为平面,所以.【考点定位】线面平行判定定理,线面垂直判定定理2.【2013江苏,理16】)如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.求证:(1)平面EFG∥平面ABC;(2)BC⊥SA.【答案】(1)详见解析;(2)详见解析3.【2014江苏,理16】如图在三棱锥中,分别为棱的中点,已知,求证(1)直线平面;(2)平面平面.【答案】证明见解析.【解析】试题分析:(1)本题证明线面平行,根据其判定定理,需要在平面内找到一条与平行的直线,由于题中中点较多,容易看出,然后要交待在平面外,在平面内,即可证得结论;(2)要证两平面垂直,一般要证明一个平面内有一条直线与另一个平面垂直,由(1)可得,因此考虑能否证明与平面内的另一条与相交的直线垂直,由已知三条线段的长度,可用勾股定理证明,因此要找的两条相交直线就是,由此可得线面垂直.4.【2016高考浙江理数改编】已知互相垂直的平面交于直线l.若直线m,n满足则直线中垂直关系是.【答案】【解析】试题分析:由题意知,.考点:空间点、线、面的位置关系.【思路点睛】解决这类空间点、线、面的位置关系问题,一般是借助长方体(或正方体),能形象直观地看出空间点、线、面的位置关系.5.【2016高考新课标2理数】是两个平面,是两条直线,有下列四个命题:(1)如果,那么.(2)如果,那么.(3)如果,那么.(4)如果,那么与所成的角和与所成的角相等.其中正确的命题有.(填写所有正确命题的编号)【答案】②③④考点:空间中的线面关系.6.【2016高考山东文数改编】已知直线a,b分别在两个不同的平面α,内,则“直线a和直线b相交”是“平面α和平面相交”的.(在充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件中选填)【答案】充分不必要条件【解析】试题分析:“直线和直线相交”“平面和平面相交”,但“平面和平面相交”“直线和直线相交”,所以“直线和直线相交”是“平面和平面相交”的充分不必要条件.考点:1.充要条件;2.直线与平面的位置关系.【名师点睛】充要条件的判定问题,是高考常考题目之一,其综合性较强,易于和任何知识点结合.本题涉及直线与平面的位置关系,突出体现了高考试题的基础性,能较好的考查考生分析问题解决问题的能力、空间想象能力等.7.【2016高考新课标Ⅲ文数】如图,四棱锥中,平面,,,,为线段上一点,,为的中点.(I)证明平面;(II)求四面体的体积.【答案】(Ⅰ)见解析;(Ⅱ).【解析】试题分析:(Ⅰ)取的中点,然后结合条件中的数据证明四边形为平行四边形,从而得到,由此结合线面平行的判断定理可证;(Ⅱ)由条件可知四面体的高,即点到底面的距离为棱的一半,由此可顺利求得结果.试题解析:(Ⅰ)由已知得,取的中点,连接,由为中点知,.......3分又,故,四边形为平行四边形,于是.因为平面,平面,所以平面.........6分(Ⅱ)因为平面,为的中点,所以到平面的距离为.....9分取的中点,连结.由得,.由得到的距离为,故,所以四面体的体积......12分考点:1、直线与平面间的平行与垂直关系;2、三棱锥的体积.【技巧点拨】(1)证明立体几何中的平行关系,常常是通过线线平行来实现,而线线平行常常利用三角形的中位线、平行四边形与梯形的平行关系来推证;(2)求三...