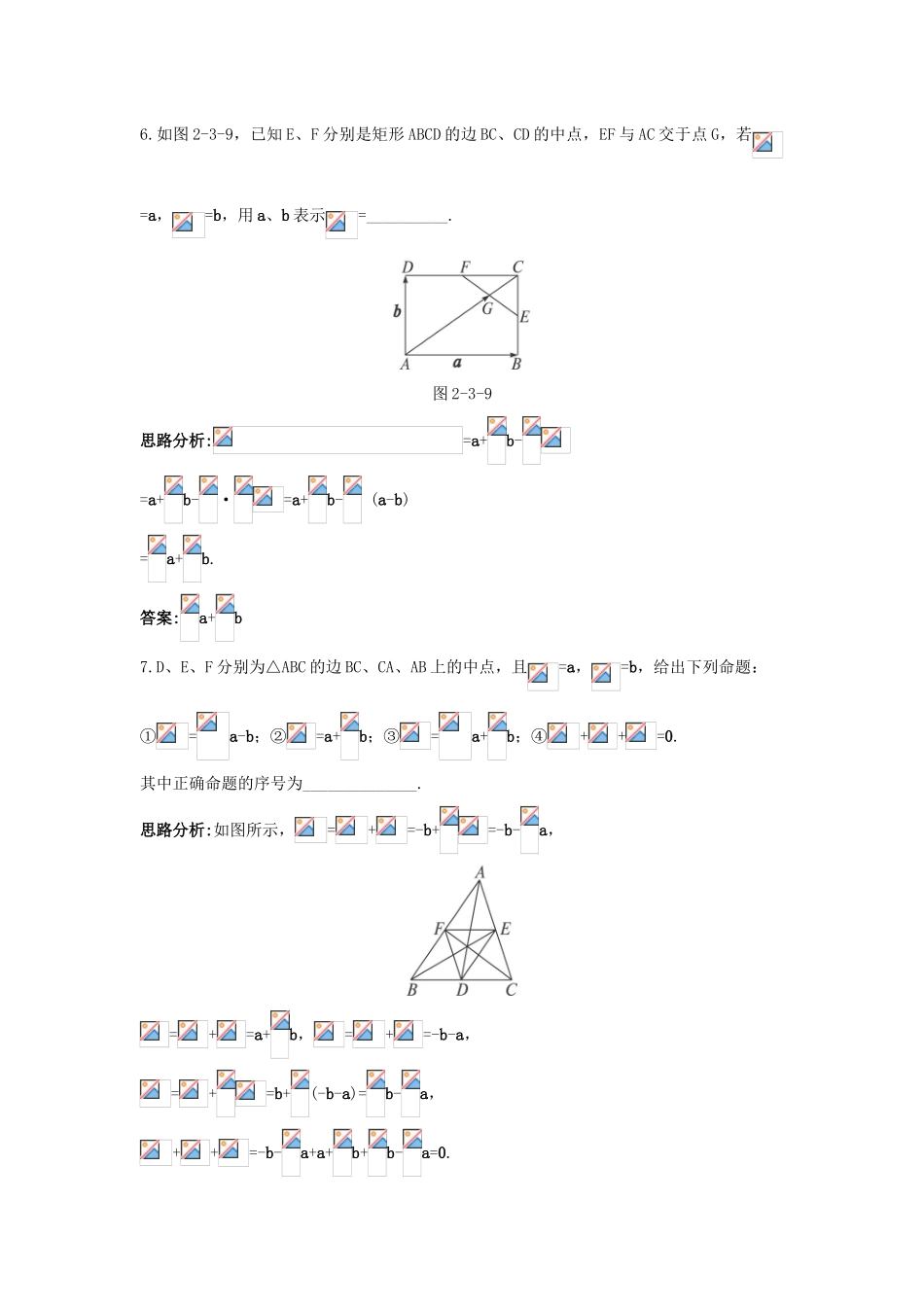
2.3.1平面向量基本定理更上一层楼基础•巩固1.已知如图2-3-8,ABCDEF是正六边形,且=a,=b,则等于()图2-3-8A.(a-b)B.(b-a)C.a+bD.(a+b)思路分析:连结AD,则=a+b,∴==(a+b).答案:D2.如果e1、e2是平面α内所有向量的一组基底,那么()A.若实数λ1、λ2使λ1e1+λ2e2=0,则λ1=λ2=0B.空间任一向量a可以表示为a=λ1e1+λ2e2,这里λ1、λ2是实数C.对实数λ1、λ2,λ1e1+λ2e2不一定在平面α内D.对平面α中的任一向量a,使a=λ1e1+λ2e2的实数λ1、λ2有无数对思路分析:平面α内任一向量都可写成e1与e2的线性组合形式,而不是空间内任一向量,故B不正确;C中的向量λ1e1+λ2e2一定在平面α内;而对平面α中的任一向量a,实数λ1、λ2是唯一的.答案:A3.下面给出了三个命题:①非零向量a与b共线,则a与b所在的直线平行;②向量a与b共线的条件是当且仅当存在实数λ1、λ2,使得λ1a=λ2b;③平面内的任一向量都可用其他两个向量的线性组合表示.其中正确命题的个数是()A.0B.1C.2D.3思路分析:命题①两共线向量a与b所在的直线有可能重合;命题③平面内的任一向量都可用其他两个不共线向量的线性组合表示.故①③都不正确.答案:B4.已知四边形ABCD是菱形,点P在对角线AC上(不包括端点A、C),则等于()A.λ(+),λ∈(0,1)B.λ(+),λ∈(0,)C.λ(-),λ∈(0,1)D.λ(-),λ∈(0,)思路分析:∵P在AC上且不包括端点A、C,∴,λ∈(0,1).由平行四边形法则+=,∴λ(+)=λ=.答案:A综合•应用5.O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足=+λ(),λ∈[0,+∞),则P的轨迹一定通过△ABC的()A.外心B.内心C.重心D.垂心思路分析:因与都为单位向量,所以λ(+)平分与的夹角,如图所示,即平分∠A,即通过△ABC的内心.答案:B6.如图2-3-9,已知E、F分别是矩形ABCD的边BC、CD的中点,EF与AC交于点G,若=a,=b,用a、b表示=__________.图2-3-9思路分析:=a+b-=a+b-·=a+b-(a-b)=a+b.答案:a+b7.D、E、F分别为△ABC的边BC、CA、AB上的中点,且=a,=b,给出下列命题:①=a-b;②=a+b;③=a+b;④++=0.其中正确命题的序号为______________.思路分析:如图所示,=+=-b+=-b-a,=+=a+b,=+=-b-a,=+=b+(-b-a)=b-a,++=-b-a+a+b+b-a=0.所以应填①②③④.答案:①②③④回顾•展望8.如图2-3-10,在△OAB中,=,=,与交于M点,设=a,=b.图2-3-10(1)用a、b表示.(2)在已知线段AC上取一点E,在线段BD上取一点F,使EF过M点.设=p,=q.求证:.(1)解:设=ma+nb,则=ma+nb-a=(m-1)a+nb,=-=b-a=-a+b.∵A、M、D三点共线,∴与共线.∴.∴m+2n=1.①而=ma+nb-a=(m-)a+nb,=-=b-a=-a+b.∵C、M、B三点共线,∴与共线.∴.∴4m+n=1.②联立①②解得m=,n=.∴=a+b.(2)证明:∵=a+b-=a+b-pa=(-p)a+b,=-=q-p=qb-pa=-pa+qb,又∵与共线,∴.∴q-pq=p.∴.