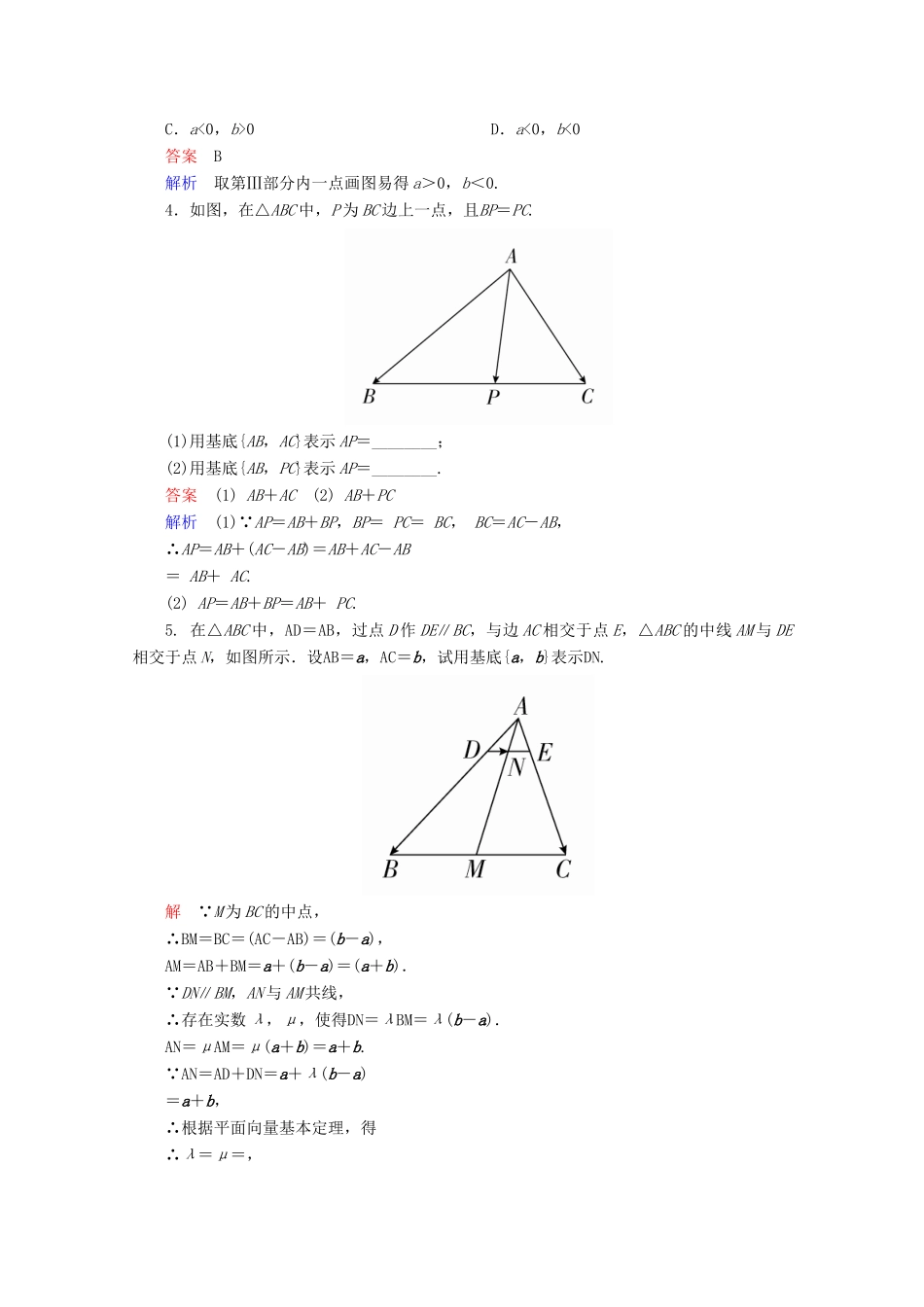
课时31平面向量基本定理知识点一平面向量基本定理的理解1.如果e1,e2是平面α内两个不共线的向量,λ,μ是实数,那么下列说法中不正确的是()①λe1+μe2可以表示平面α内的所有向量;②对于平面α内任意一个向量a,使得a=λe1+μe2的实数对(λ,μ)有无穷多个;③若向量λ1e1+μ1e2与λ2e1+μ2e2共线,则有且只有一个实数λ,使得λ1e1+μ1e2=λ(λ2e1+μ2e2);④若实数λ,μ使得λe1=μe2,则λ=μ=0.A.①②B.②③C.③④D.②答案B解析由平面向量基本定理可知,①④正确.对于②,由平面向量基本定理可知,一旦一个平面的基底确定,那么任意一个向量在此基底下的实数对是唯一的,故②不正确.对于③,当两向量均为零向量,即λ1=λ2=μ1=μ2=0时,λ有无穷多个,故③不正确.2.若{e1,e2}是平面α内的一组基底,则下列四组向量能作为平面α的一组基底的是()A.{e1-e2,e2-e1}B.{2e1+e2,e1+e2}C.{2e2-3e1,6e1-4e2}D.{e1+e2,e1-e2}答案D解析对于选项A,e1-e2=-(e2-e1),所以(e1-e2)∥(e2-e1),故该组向量不能作为该平面的基底;对于选项B,2e1+e2=2,所以(2e1+e2)∥,故该组向量不能作为该平面的基底;对于选项C,2e2-3e1=-(6e1-4e2),所以(2e2-3e1)∥(6e1-4e2),故该组向量不能作为该平面的基底;对于选项D,显然e1+e2与e1-e2不共线,故该组向量能作为该平面的基底.知识点二用基底表示向量3.如图所示,平面内的两条相交直线OP1和OP2将该平面分割成四个部分Ⅰ,Ⅱ,Ⅲ,Ⅳ(不包括边界).若OP=aOP1+bOP2,且点P落在第Ⅲ部分,则实数a,b满足()A.a>0,b>0B.a>0,b<0C.a<0,b>0D.a<0,b<0答案B解析取第Ⅲ部分内一点画图易得a>0,b<0.4.如图,在△ABC中,P为BC边上一点,且BP=PC.(1)用基底{AB,AC}表示AP=________;(2)用基底{AB,PC}表示AP=________.答案(1)AB+AC(2)AB+PC解析(1) AP=AB+BP,BP=PC=BC,BC=AC-AB,∴AP=AB+(AC-AB)=AB+AC-AB=AB+AC.(2)AP=AB+BP=AB+PC.5.在△ABC中,AD=AB,过点D作DE∥BC,与边AC相交于点E,△ABC的中线AM与DE相交于点N,如图所示.设AB=a,AC=b,试用基底{a,b}表示DN.解 M为BC的中点,∴BM=BC=(AC-AB)=(b-a),AM=AB+BM=a+(b-a)=(a+b). DN∥BM,AN与AM共线,∴存在实数λ,μ,使得DN=λBM=λ(b-a).AN=μAM=μ(a+b)=a+b. AN=AD+DN=a+λ(b-a)=a+b,∴根据平面向量基本定理,得∴λ=μ=,∴DN=(b-a)=-a+b.知识点三平面向量基本定理的应用6.已知O,A,M,B为平面上四点,且OM=λOB+(1-λ)·OA,实数λ∈(1,2),则()A.点M在线段AB上B.点B在线段AM上C.点A在线段BM上D.O,A,M,B四点一定共线答案B解析由题意得OM-OA=λ(OB-OA),即AM=λAB.又λ∈(1,2),所以点B在线段AM上.故选B.7.在平行四边形ABCD中,E和F分别是边CD和BC的中点.若AC=λAE+μAF,其中λ,μ∈R,则λ+μ=________.答案解析设AB=a,AD=b,则AE=a+b,AF=a+b.又 AC=a+b,∴AC=(AE+AF),即λ=μ=.∴λ+μ=.8.已知a,b是两个不共线的向量,若它们起点相同,a,b,t(a+b)三个向量的终点在一条直线上,则实数t=________.答案解析如图, a,b,t(a+b)三个向量的终点在一条直线上,∴存在实数λ使t(a+b)-b=λ,即(t-λ)a=b.又 a,b不共线,∴t-λ=0且-λ-t=0,解得t=.9.如图,已知三点O,A,B不共线,且OC=2OA,OD=3OB,设OA=a,OB=b.(1)设AD与BC交于点E,试用a,b表示向量OE;(2)设线段AB,OE,CD的中点分别为L,M,N,试证明L,M,N三点共线.解(1) B,E,C三点共线,∴存在实数x,使OE=xOC+(1-x)OB=2xa+(1-x)b.①同理, A,E,D三点共线,∴存在实数y,使OE=ya+3(1-y)b.②由①②,得解得x=,y=.∴OE=a+b.(2)证明: OL=,OM=OE=,ON=(OC+OD)=,∴MN=ON-OM==,ML=OL-OM=,∴MN=6ML,∴L,M,N三点共线.易错点忽略两个向量作为基底的条件10.已知e1≠0,λ∈R,a=e1+λe2,b=2e1,则a与b共线的条件为()A.λ=0B.e2=0C.e1∥e2D.e1∥e2或λ=0易错分析若认为e1,e2是一组...