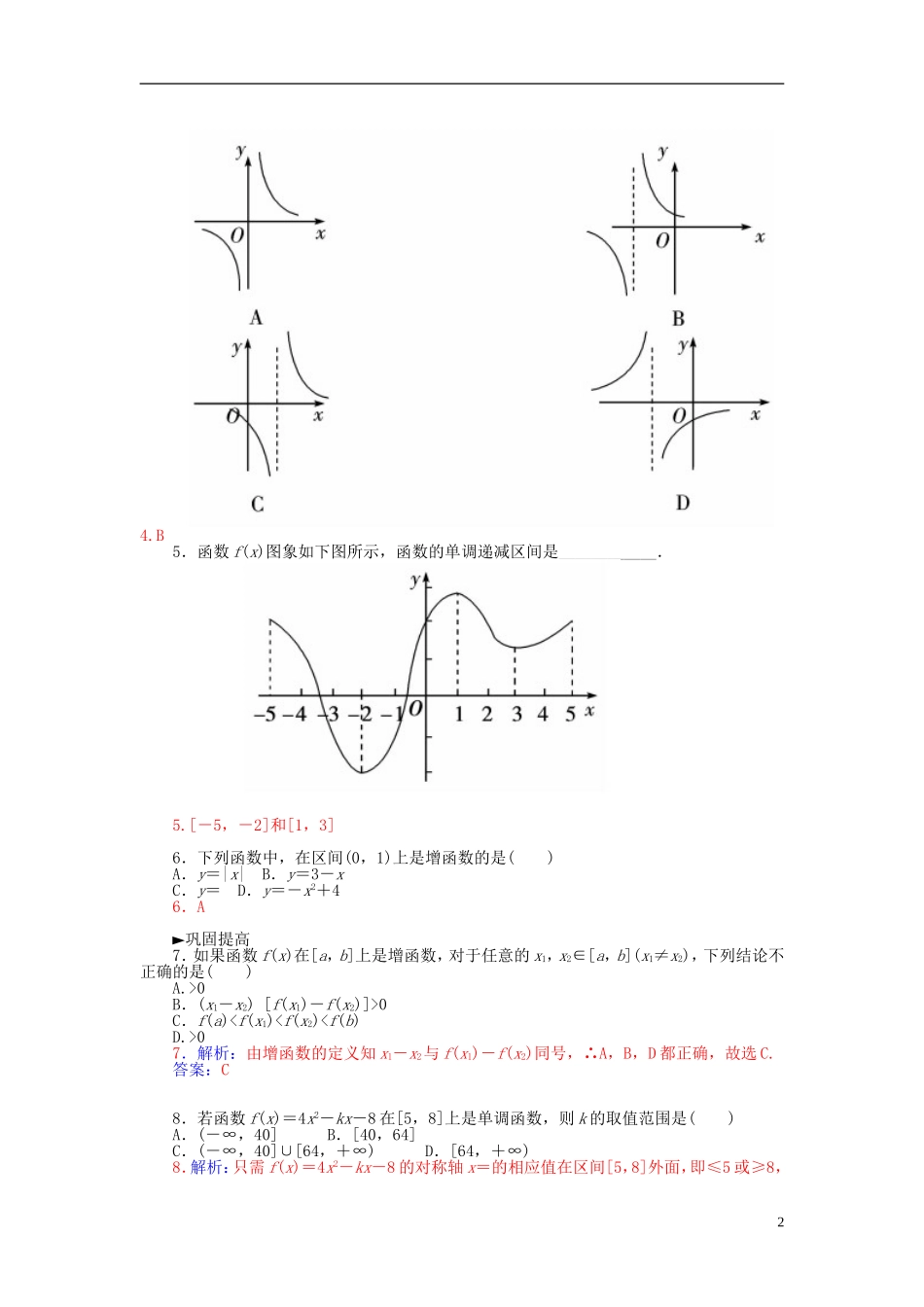
【金版学案】2015-2016高中数学1.3.1函数的单调性练习新人教A版必修11.如果函数f(x)对区间D内的任意x1,x2,当x1<x2时都有f(x1)<f(x2),则f(x)在D内是增函数;当x1<x2时都有f(x1)>f(x2),则f(x)在D内是减函数.例如:若f(x)=2x-1,能证明出函数f(x)在R上为增函数吗?____.2.函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;必须是对于区间D内的任意两个自变量x1,x2;当x1<x2时,总有f(x1)<f(x2)[或f(x1)>f(x2)].例如:f(x)是R上的单调函数,若f(3)>f(2),则y=f(x)是R上的单调____函数;若f(3)>f(2),则y=f(x)是R上的单调增函数吗?____.3.若函数y=f(x)在区间I上是单调增函数或是单调减函数,那么就说函数y=f(x)在区间I上具有单调性,单调增区间和单调减区间统称为单调区间.4.若函数y=f(x)是R上的增函数,当a>b时,则f(a)____f(b);若函数y=f(x)是R上的减函数,当a>b时,则f(a)____f(b).5.函数f(x)=x2+2x+11的单调增区间是________,基础梳理1.能2.递增不是4.><5.[-1,+∞)1.如果f(x)在区间D上是单调函数,则函数f(x)是增函数(减函数)的说法正确吗?1.解析:不正确.函数的单调性是函数的局部性质,所以必须说明函数在哪个区间上是增(减)函数.2.函数f(x)在区间D上是增(减)函数,对于任意x1,x2∈D,则有“若x1<x2,则f(x1)<f(x2)[f(x1)>f(x2)]”,反之是否也成立呢?2.解析:成立.即函数f(x)在D上是增(减)函数,对于∀x1,x2∈D,若f(x1)<f(x2)[f(x1)>f(x2)],则x1<x2,这个性质从函数单调性的图形定义中能形象地体现出来.1.下列结论正确的是()A.函数y=-2x在R上为增函数B.函数y=x2在R上为增函数C.函数y=在定义域内为减函数D.函数y=在(-∞,0)上为减函数2.函数y=-2x2+3x的单调减区间是()A.[0,+∞)B.(-∞,0)C.D.3.若f(x)在R上是增函数,且f(x1)>f(x2),则x1,x2的大小关系为________.自测自评1.解析:借助图象知D正确.故选D.答案:D2.解析:借助图象得y=-2x2+3x的单调减区间是,故选D.答案:D3.解析: f(x)在R上是增函数,且f(x1)>f(x2),∴x1>x2.答案:x1>x2►基础达标1.使一次函数f(x)=kx+b为增函数的一个条件是()A.k<0B.k≤0C.k>0D.k≥01.C2.下列说法正确的是()A.反比例函数y=在区间(0,+∞)上是减函数B.二次函数y=ax2+bx+c图象开口向上C.反比例函数y=是R上的减函数D.一次函数f(x)=-2x+b是R上的减函数2.D3.若函数y=f(x)在区间(a,b)内是增函数,在区间(b,c)内也是增函数,则函数y=f(x)在区间(a,b)∪(b,c)内()A.必是增函数B.必是减函数C.是增函数或减函数D.无法确定单调性3.D4.函数y=的大致图象只能是()14.B5.函数f(x)图象如下图所示,函数的单调递减区间是____________.5.[-5,-2]和[1,3]6.下列函数中,在区间(0,1)上是增函数的是()A.y=|x|B.y=3-xC.y=D.y=-x2+46.A►巩固提高7.如果函数f(x)在[a,b]上是增函数,对于任意的x1,x2∈[a,b](x1≠x2),下列结论不正确的是()A.>0B.(x1-x2)[f(x1)-f(x2)]>0C.f(a)07.解析:由增函数的定义知x1-x2与f(x1)-f(x2)同号,∴A,B,D都正确,故选C.答案:C8.若函数f(x)=4x2-kx-8在[5,8]上是单调函数,则k的取值范围是()A.(-∞,40]B.[40,64]C.(-∞,40]∪[64,+∞)D.[64,+∞)8.解析:只需f(x)=4x2-kx-8的对称轴x=的相应值在区间[5,8]外面,即≤5或≥8,2∴k≤40或k≥64.答案:C9.已知f(x)在(0,+∞)上是减函数,判断f(a2-a+1)与f的大小关系.9.解析: a2-a+1=+≥,且f(x)在(0,+∞)上是减函数,∴f(a2-a+1)≤f.10.设函数f(x)=x+,试讨论f(x)在(0,+∞)上的单调性.10.分析:根据函数单调性定义,作差f(x1)-f(x2)后通过x在不同区间取值对差的符号影响进行讨论.解析:设0<x1<x2,则f(x1)-f(x2)=-=. x1-x2<0,x1x2>0,∴f(x1)-f(x2)的符号由x1x2-1确定.设f(x)在(0,a]上单调,则对任意x1,x2∈(0,a]恒有x1x2-1<0,而在x1,x2∈[a,+∞)时,恒有x1x2-1>0,∴a2-1=0,a=1.∴当x1,x2∈(0,1...