高一数学人教新课标版（B）下学期期末试卷VIP免费

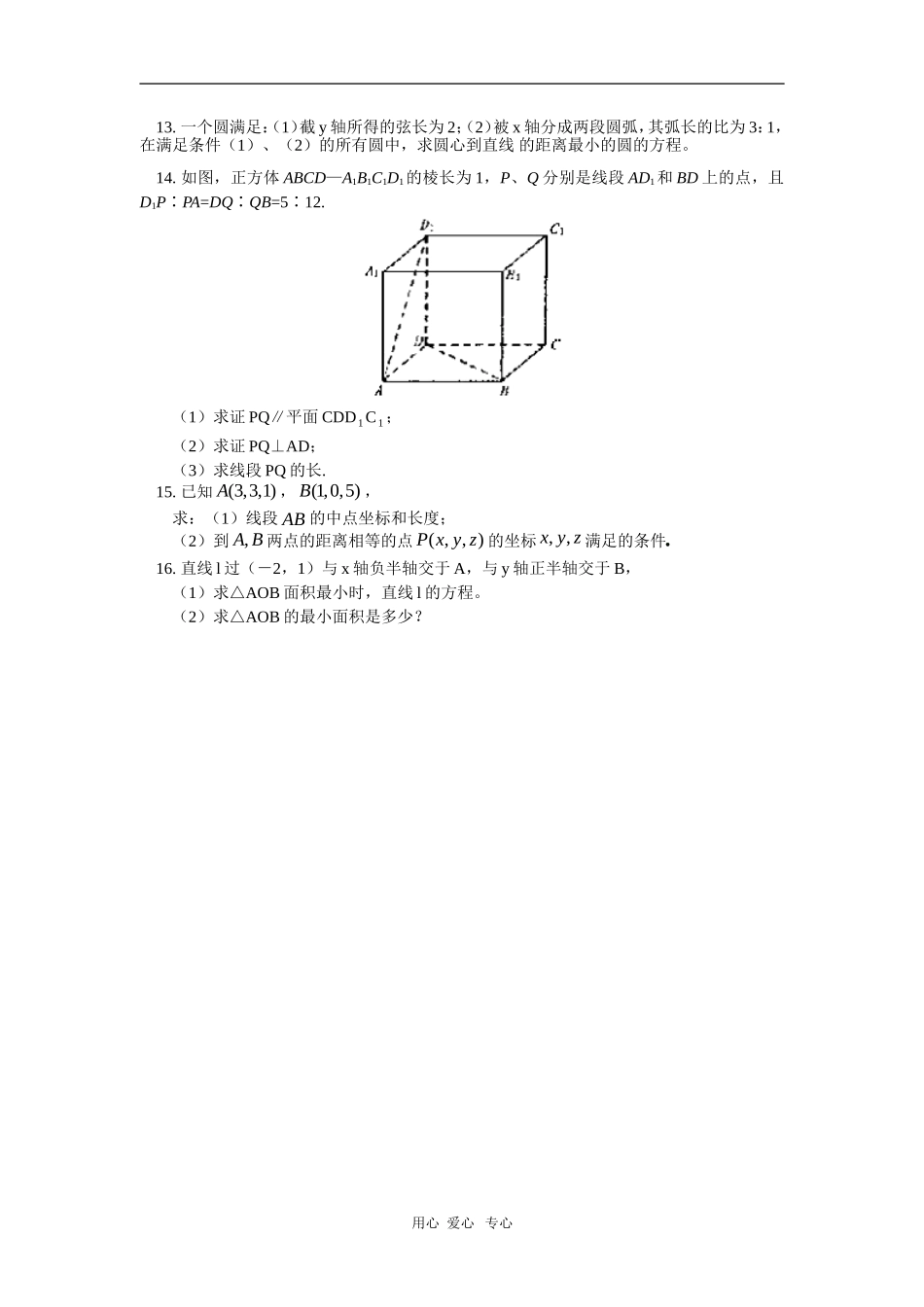
高一数学人教实验B版期末试卷（答题时间：90分钟）一、选择题（本大题共8小题，每小题5分，共40分）1.设、为两个不同的平面，lm、为两条不同的直线，且,lm，有如下的两个命题：①若∥，则l∥m；②若l⊥m，则⊥.那么A.①是真命题，②是假命题B.①是假命题，②是真命题C.①②都是真命题D.①②都是假命题2.以原点为圆心，且截直线01543yx所得弦长为8的圆的方程是（）A.522yxB.2522yxC.422yxD.1622yx3.设a、b是两条不同的直线，、是两个不同的平面，则下列命题中正确的是（）A.若//ab，//a，则//bB.若，//a，则aC.若，a，则//aD.若ab，a，b，则4.直线02y3ax与直线02yx2a相互垂直，则实数a的值是（）A.–1B.3C.–1或3D.05.直线axay1的图象是（）3.D23.C33.B21.A)(xy,3y)2x(y,x.622的最大值是那么满足等式如果实数7.在圆x2＋y2＝4上与直线4x＋3y－12=0距离最小的点的坐标是（）A.（85，65）B.（85，－65）C.（－85，65）D.（－85，－65）8.设0m，则直线0m1yx2与圆myx22的位置关系为A.相切B.相交C.相切或相离D.相交或相切二、填空题（本题共4小题，每小题5分，共20分）9.已知△ABC的三个顶点A（1，4），B（－2，3），C（4，－5），则△ABC外接圆的方程为___________。10.长方体的一个顶点上的三条棱长分别为1,2,3，该长方体的顶点都在同一个球面上，则这个球的表面积为11.过点C（－1，1）和D（1，3），圆心在x轴上的圆的方程是___________________。12.直线032yx关于定点)2,1(M1对称的直线方程是_______________三、解答题（本大题共4题，共40分）1用心爱心专心13.一个圆满足：（1）截y轴所得的弦长为2；（2）被x轴分成两段圆弧，其弧长的比为3：1，在满足条件（1）、（2）的所有圆中，求圆心到直线的距离最小的圆的方程。14.如图，正方体ABCD—A1B1C1D1的棱长为1，P、Q分别是线段AD1和BD上的点，且D1P∶PA=DQ∶QB=5∶12.（1）求证PQ∥平面CDD1C1；（2）求证PQ⊥AD；（3）求线段PQ的长.15.已知(3,3,1)A，(1,0,5)B，求：（1）线段AB的中点坐标和长度；（2）到,AB两点的距离相等的点(,,)Pxyz的坐标,,xyz满足的条件奎屯王新敞新疆16.直线l过（－2，1）与x轴负半轴交于A，与y轴正半轴交于B，（1）求△AOB面积最小时，直线l的方程。（2）求△AOB的最小面积是多少？用心爱心专心【试题答案】一、选择题（本大题共8小题，每小题5分，共40分）1.解：C,A)1(m//l//,m,l是假命题，故可排除推不出②也是假命题。故选择D2.B3.D4.C5.D6..33)2(003)2(),(2222DyxOxykOPyxyxP，故选相切的直线的斜率为且与圆过原点的斜率上任意一点，则直线为圆解：设7.解：图解法:在同一直角坐标系中作出圆x2＋y2＝4和直线4x＋3y－12=0后，由图可知距离最小的点在第一象限内，所以选A.直接法：先求得过原点的垂线，再与已知圆相交而得.8.C二、填空题（本题共4小题，每小题5分，共20分）9.解：设圆的方程为：0FEyDxyx22（0F4ED22） 圆过三点为A（1，4），B（－2，3），C（4，－5），∴0FE5D425160FE3D2940FE4D161，即041FE5D4013FE3D2017FE4D，解得：D=－2，E=2，F=－23，∴所求外接圆的方程是023y2x2yx22。10.1411.（x－2）2+y2=1012.解：设点),(yx关于)2,1(的对称点为),(yx，则xx2，yy4。∴03)4()2(2yx即：052yx三、解答题（本大题共4题，共40分）13.解：设圆的圆心为，半径为r，则点P到x轴、y轴的距离分别为由题设知圆P截x轴所得劣弧所对的圆心角为90°，知圆P截x轴所得的弦长为，故。又圆P截y轴所得的弦长为2，所以有从而得又点到直线的距离为所以有当且仅当时等号成立，此时从而d取最小值，因此有解此方程组得，或由于，知∴所求圆的方程是或14.（1）证明：在平面AD1内，作PP1∥AD与DD1交于点P1，在平面AC内，作QQ1∥BC用心爱心专心交CD于点Q1，连结P1Q1. 1251QBDQPAPD...