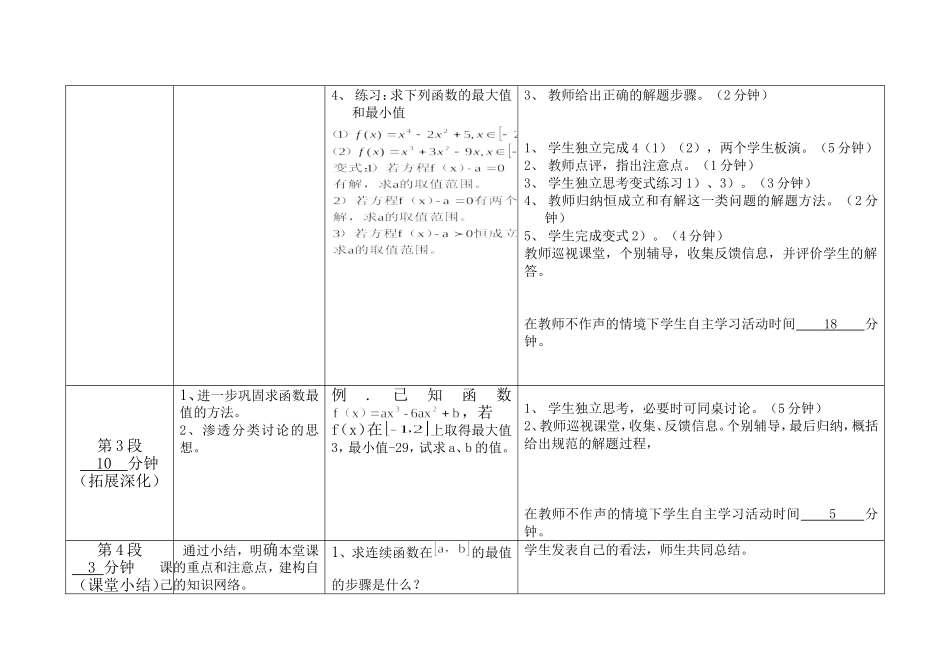
课堂45分钟分段式模块教学设计课题名称函数的最大(小)值与导数时间段落教学目标内容模块教学过程与方法第1段7分钟(作业讲评)1、通过作业中的错误矫正,进一步明确极值和极值点这两个概念的不同之处。2、能叙述求极值的步骤作业本P15,6、10P16,11、(2)1、上课前由三个学生在黑板上书写好自己的错误解答。2、全班同学对照自己的作业本,找出同学的错误。三个学生讲评错误之处,并提出正确解答。(4分钟)3、教师点评分析错误形成原因,指出注意点。(3分钟)在教师不作声的情境下学生自主学习活动时间4分钟。第2段25分钟(新课学习)1、能借助图像,找出连续函数在上的最大值,最小值,并能自主归纳出求连续函数f(x)在上的最值的步骤。2、90%的学生能求不含参数的三次函数在上的最值。3、通过变式练习,能把有解和恒成立问题转化为求函数的最值问题。4、渗透化归与转化的思想。1、观察29页1.3-13图像,口答:①找出f(x)在上的极大值、极小值;②找出f(x)在上的最大值、最小值;③没有给出函数图像的情况下,怎样才能判断出最大值、最小值。2、归纳求f(x)在上的最值的步骤。3、复习28页例4变式:求函数f(x)在上的最大值和最小值。1、学生观察图像,并回答问题。(2分钟)2、教师引导总结、归纳出求连续函数y=f(x)在上的最值的步骤。(2分钟)1、学生看书28页,并求解变式。(2分钟)2、问实际求连续函数y=f(x)在上的最值时哪些步骤可以省略,学生思考。(2分钟)4、练习:求下列函数的最大值和最小值3、教师给出正确的解题步骤。(2分钟)1、学生独立完成4(1)(2),两个学生板演。(5分钟)2、教师点评,指出注意点。(1分钟)3、学生独立思考变式练习1)、3)。(3分钟)4、教师归纳恒成立和有解这一类问题的解题方法。(2分钟)5、学生完成变式2)。(4分钟)教师巡视课堂,个别辅导,收集反馈信息,并评价学生的解答。在教师不作声的情境下学生自主学习活动时间18分钟。第3段10分钟(拓展深化)1、进一步巩固求函数最值的方法。2、渗透分类讨论的思想。例.已知函数,若f(x)在上取得最大值3,最小值-29,试求a、b的值。1、学生独立思考,必要时可同桌讨论。(5分钟)2、教师巡视课堂,收集、反馈信息。个别辅导,最后归纳,概括给出规范的解题过程,在教师不作声的情境下学生自主学习活动时间5分钟。第4段3分钟(课堂小结)通过小结,明确本堂课课的重点和注意点,建构自己的知识网络。1、求连续函数在的最值的步骤是什么?学生发表自己的看法,师生共同总结。2、有解问题和恒成立问题如何求解?3、分类讨论时分类的依据是什么?备课收获1、更加明确本堂课所需要达到的教学目标。2、能从学生的角度考虑解决问题大约所需要的时间,使课堂结构更加合理。