第一讲实数及其运算VIP免费

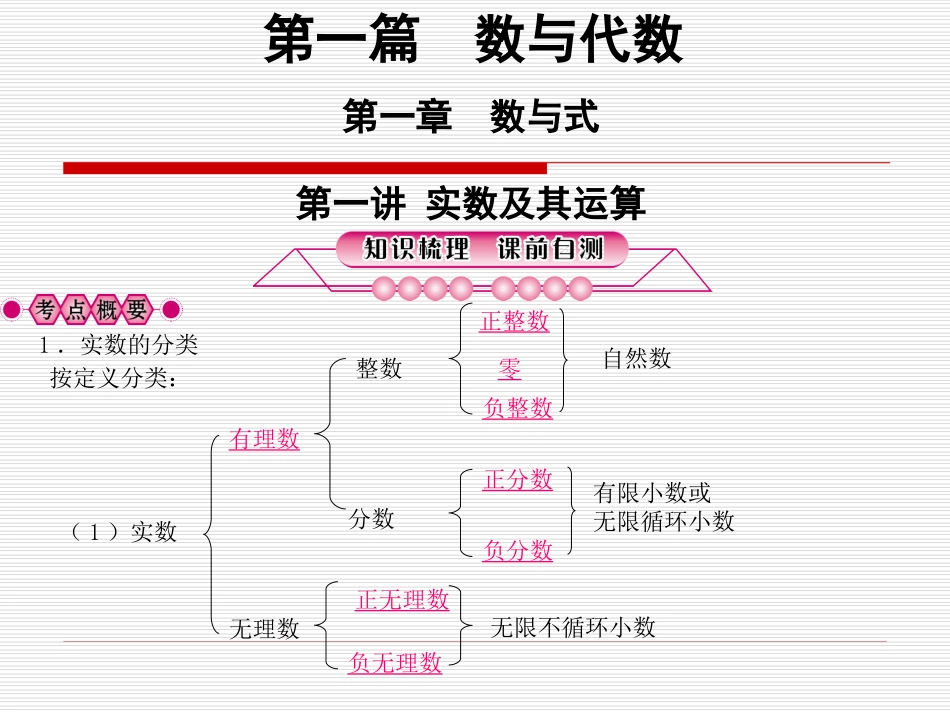
第一篇数与代数第一章数与式1．实数的分类按定义分类：有理数无理数（1）实数无限不循环小数自然数有限小数或无限循环小数整数分数正分数负分数正整数零负整数正无理数负无理数第一讲实数及其运算(2)根据需要，我们也可以按正负分类进行分类，如：实数【提醒】(1)任何分数都是有理数，如，－；(2)0既不是正数，也不是负数，但0是自然数．2．实数的有关概念(1)数轴：规定了__原点__，__正方向__和__单位长度__的直线叫做数轴．数轴上所有的点与全体__实数__一一对应．(2)相反数：只有__符号__不同，而__绝对值__相同的两个数称为互为相反数．若a、b互为相反数，则a＋b＝__0__．(3)倒数：1除以一个不等于零的实数所得的_商_，叫做这个数的倒数．若a、b互为倒数，则ab＝_1_．(4)绝对值：在数轴上，一个数对应的点离开原点的_距离_叫做这个数的绝对值．|a|＝a（a>0）0（a＝0）－a（a<0）|a|是一个非负数，即|a|__≥0__．(5)科学记数法，近似数：科学记数法就是把一个数表示成__a×10n__的形式(其中1≤|a|<10，n为整数)；一个近似数，__四舍五入__到哪一位，就说这个数精确到哪一位．【提醒】对于带计数单位的近似数，由近似数的位数和后面的单位共同确定．如3.618万，数字8实际上是十位上的数字，即精确到十位．(6)平方根，算术平方根，立方根：如果x2＝a，那么x叫做a的平方根，记作____；正数a的正的平方根，叫做这个数的算术平方根；如果x3＝a，那么x叫做a的立方根，记作____．a3a(7)非负数：正数和零叫做非负数．常见的非负数：|a|，a2，(a≥0，a可代表一个数或一个式)．a非负数的性质：若几个非负数的和等于零，则这几个数都为0.3．实数的运算(1)任何非零数的零次幂都等于1，即__a0＝1(a≠0)__；任何不等于零的数的－p次幂，等于这个数p次幂的倒数，即__a－p＝(a≠0，p为正整数)__．pa1(2)实数的运算顺序是先算__乘方和开方__，再算__乘除__，最后算__加减__．如果有括号，先算__小括号__，再算__中括号__，最后算__大括号__．同级运算应__从左到右，依次进行__．【提醒】(1)零指数、负整数指数的意义，防止以下错误：①3－2＝；②2a－2＝；(2)遇到绝对值一般要先去掉绝对值符号，再进行计算；(3)无论何种运算，都要注意先定符号后运算．91221a4．实数的大小比较代数比较规则：正数__大于__零，负数__小于__零，正数__大于__一切负数；两个正数，绝对值大的较大；两个负数，绝对值大的反而__小__．几何比较规则：在数轴上表示的两个实数，__右边__的数总是大于_左边_的数．(1)分类讨论思想：分类讨论思想是“化整为零，各个击破，再积零为整”的数学策略．分类注意按一定的标准进行；分类既不能遗漏，也不能交叉重复．(2)数形结合思想：数形结合思想是指将数(量)与(图)形结合起来进行分析、研究、解决问题的一种思想策略．数形结合使问题化难为易、化繁为简．(3)化归思想：化归也称转化，是指将未知的、陌生的、复杂的问题通过演绎归纳转化为已知的、熟悉的、简单的问题，从而使问题顺利解决的数学思想．关键是确定合理、可行的转化目标，掌握基本的方法、步骤．1．(2013·嘉兴)－2的相反数是(A)(B)2．(2013·绍兴)地球半径约为6400000米，这个数用科学记数法表示为A．0.64×107B．6.4×106C．6.4×105D．64×105(D)3．(2012·温州)给出四个数－1，0，0.5，，其中为无理数的是4．(2011·金华)如图，若A是实数a在数轴上所对应的点，则关于a，－a，1的大小关系表示正确的是A．a<1<－aB．a<－a<1C．1<－a