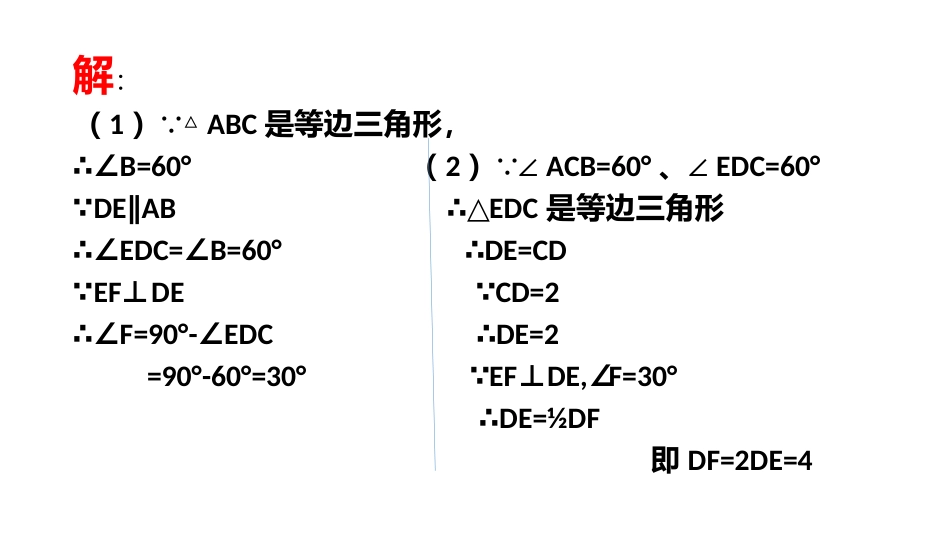
15.3等腰三角形典型例题解析题型一求线段或角度1、如图所示,在等边三角形ABC中,点D、E分别在边BC、AC上,且DE∥AB,过点E作EF⊥DE,交BC延长线于点F。(1)求∠F的度数,(2)若CD=2,求DF的长。解:(1) △ABC是等边三角形,∴∠B=60°(2) ∠ACB=60°、∠EDC=60° DEABEDC∥∴△是等边三角形∴∠EDC=B=60°DE=CD∠∴ EFDECD=2⊥ ∴∠F=90°-EDCDE=2∠∴=90°-60°=30°EFDE,F=30° ⊥∠∴DE=½DF即DF=2DE=4题型二等腰(等边)三角形判定的应用2、如图所示,AD是△ABC的角平分线,DE,DF分别垂直AB,AC于E,F连接EF,求证△AEF是等腰三角形。证明: AD是△ABC的角平分线∴∠BAD=∠CAD又 DE,DF分别垂直AB、AC于E、F∴∠AED=∠AFD=90°又 AD=AD∴△AED≌△AFD∴AE=AF,即△AEF是等腰三角形题型三等腰(等边)三角形性质的应用3、如图所示D是△ABC边BC延长线上一点,且CD=CA,E是AD的中点,CF平分∠ACB交AB于F。求证CE⊥CF证明: CA=CD,E是AD的中点∴∠ACE=∠DCE CF平分∠ACB∴∠ACF=∠BCF ∠ACE+∠DCE+∠ACF+∠BCF=180°∴∠ACE+∠ACF=90°即∠ECF=90°∴CE⊥CF4、如图所示,△ABC和△ADE都是等边三角形,连接CD,BE.求证:CD=BE题型四含30°的直角三角形性质的应用5、如图所示,在△ABC中,AD交边BC于点D,∠BAD=15°,∠ADC=4∠BAD,DC=2BD(1)求∠B的度数(2)求证∠CAD=∠ABD解:(1) ∠BAD=15°,∠ADC=4BAD∠∴∠ADC=60°B=60°-15°=45°∠((2)证明:过C作CEAD⊥于E,连接EB. ∠ECD=90°-60°=30°∴DC=2ED, DC=2BD,∴ED=BD,∴∠DBE=DEB=ECD=30°∠∠,∴∠EBA=45°-30°=15°=BAD∠,∴AE=EC=EB,∴∠CAD=B=45°∠.题型五等腰三角形中的分类讨论6、等腰三角形的一个角为30°,求其他两角。解:当30°的角为顶角时,其余两角为75°;当30°的角为底角时,其余两角为30°;120°。7、已知等腰三角形一边的长为4,另一边的长为9,求它的周长。解:①当以4为腰长时,底边长为9, 4+4<9,不能构成三角形所以此情况不存在。②当以4为底边长时,腰长为9,此时4+9>9,能构成三角形,周长为4+9+9=22题型六实际应用题8、有一个三角形支架如图所示,AB=AC,小明过点A和BC边的中点D又架了一个细木条,经测量∠B=30°,你在不用任何测量工具的前提下,能得到∠BAD和∠ADC的度数吗?解: AB=AC,D是BC的中点∴∠B=∠C,∠BAD=∠CAD=∠BAC,AD⊥BC½又∠BAC=180°-2∠B=120°∴∠BAD=60°,∠ADC=90°题型七学科综合9、如图所示,DE是△ABC边AB的垂直平分线,分别交AB,BC于D,E,AE平分∠BAC,设∠B=x°,∠C=y°。(1)求y随x变化的函数关系式,并写出x的取值范围;(2)请讨论△ABC为等腰三角形时,∠B的度数。解:(1) DE垂直平分AB,∴AE=BE∴∠BAE=∠B=x°又 AE平分∠BAC∴∠BAC=2∠BAE=2x°∴y=180-3x(0<x<180)(2)显然AC≠BC,若AB=AC,此时x=y,即180-3x=x,解得x=45;若AB=BC,则此时2x=y即180-3x=2x解得x=36∴当△ABC为等腰三角形时,∠B为45°或36°题型八与等腰三角形有关的开放型试题10、如图所示,在△ABC中,D,E分别是AB,AC上的点,BD与CE交于点O,给出下列四个条件:①∠ECO=∠DBO,②∠BDO=∠CEO,③BE=CD,④OB=OC。(1)上述四个条件中,哪两个条件可以判定△ABC是等腰三角形(用序号写出所有的情况);(2)选(1)中的一种情形,求证△ABC是等腰三角形。题型九等腰三角形有关的一题多解11、如图(1)所示,已知△ABC为等边三角形,延长BC到D,延长BA到E,并且使AE=BD,连接CE,DE,求证ED=EC证法1证法2:过E作EF∥AC交BD延长线于F,如图(2)所示,则△BEF为等边三角形,以下同证法1(2)题型十与等腰三角形有关的动态题12、如图所示,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。(1)写出O到△ABC三个顶点A,B,C距离之间的关系;(2)如果点M,N分别在线段AB,AC上移动,移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。(1)(2)解:(1) 在Rt△ABC中,∠BAC=90°,O为BC的中点,如图(1)所示,连接OA,则△AOB和△AOC都是等腰直角三角形,∴OA=BC=OB=OC,即OA=OA=OC;(2)△OMN是等腰直角三角形,理由: AC=AB,OB=...