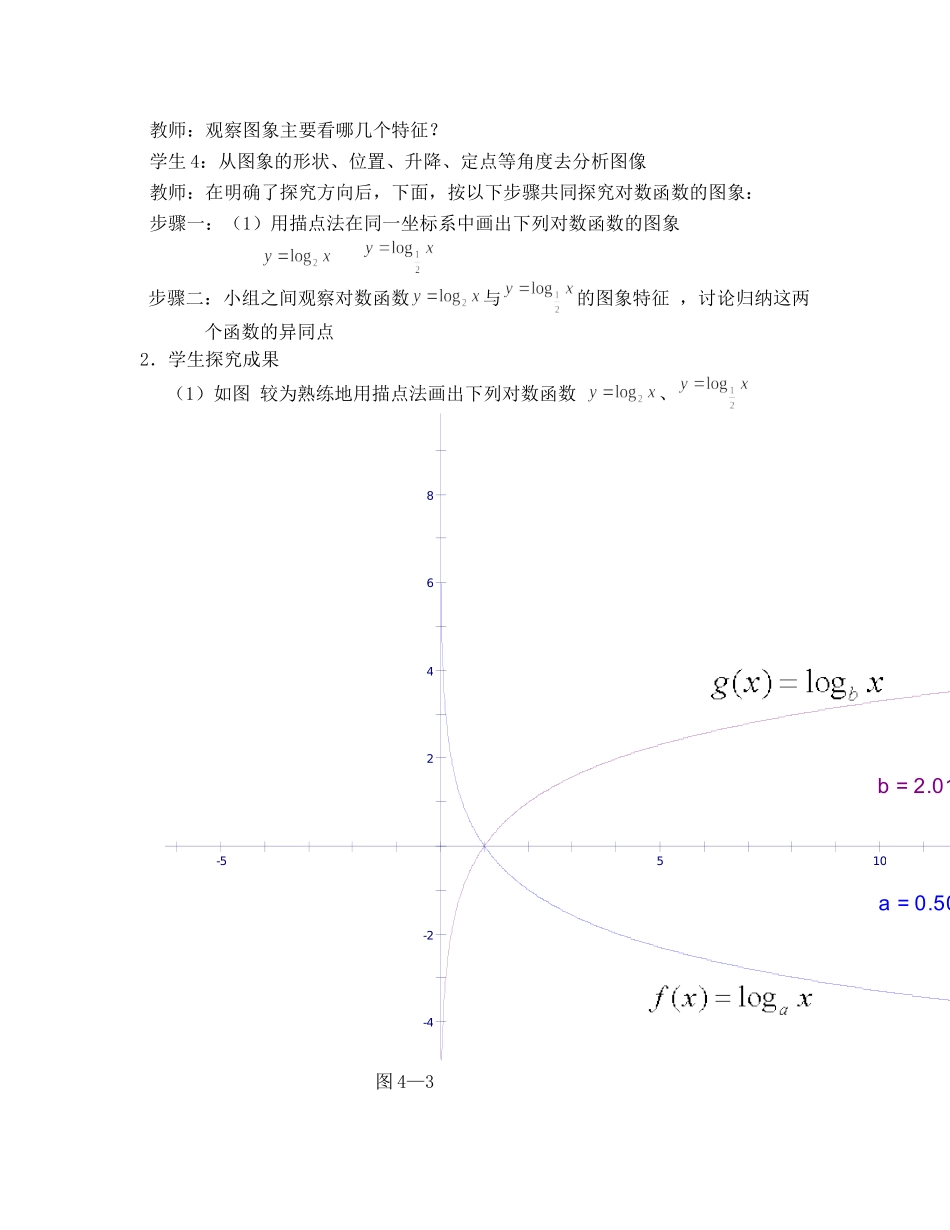
对数函数及其性质(1)教学设计来宾高级中学钟信一、教材分析本小节选自《普通高中课程标准数学教科书-数学必修(一)》(人教版)第二章基本初等函数(1)2.2.2对数函数及其性质(第一课时),主要内容是学习对数函数的定义、图象、性质及初步应用。对数函数是继指数函数之后的又一个重要初等函数,无论从知识或思想方法的角度对数函数与指数函数都有许多类似之处。与指数函数相比,对数函数所涉及的知识更丰富、方法更灵活,能力要求也更高。学习对数函数是对指数函数知识和方法的巩固、深化和提高,也为解决函数综合问题及其在实际上的应用奠定良好的基础。二、学生学习情况分析刚从初中升入高一的学生,仍保留着初中生许多学习特点,能力发展正处于形象思维向抽象思维转折阶段,但更注重形象思维。由于函数概念十分抽象,又以对数运算为基础,同时,初中函数教学要求降低,初中生运算能力有所下降,这双重问题增加了对数函数教学的难度。教师必须认识到这一点,教学中要控制要求的拔高,关注学习过程。三、设计理念本节课以建构主义基本理论为指导,以新课标基本理念为依据进行设计的,针对学生的学习背景,对数函数的教学首先要挖掘其知识背景贴近学生实际,其次,激发学生的学习热情,把学习的主动权交给学生,为他们提供自主探究、合作交流的机会,确实改变学生的学习方式。四、教学目标1.通过具体实例,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,体会对数函数是一类重要的函数模型;2.画出具体对数函数的图象,探索并了解对数函数的单调性与特殊点;3.通过比较、对照的方法,引导学生结合图象类比指数函数,探索研究对数函数的性质,培养学生运用函数的观点解决实际问题。五、教学重点与难点重点是掌握对数函数的图象和性质,难点是底数对对数函数值变化的影响.六、教学过程设计教学流程:类比、发现问题→引出课题→函数图象→函数性质→问题解决→归纳小结(一)熟悉背景、引入课题现在有一张纸,我把这张纸对折一次就变成了两层;对折两次就变成了四层。如果我们设把纸对折的次数为x,对折后纸的层数为y,那么,试建立y关于x的函数关系式。提问:教师:如果对折后的纸有4层,那对折了多少次?学生:2次教师:如果对折后的纸有8层,那对折了多少次?学生:3次教师:16层呢?32层呢?学生:4层和5层教师:我们可以发现:关于也可以建立一个函数,首先将的指数形式化成对数形式:,这里的每一个都有唯一的和它对应,说明这是一个函数,为了用以书写,我们将这个函数改写为1.引导学生观察这个函数的特征:含有对数符号,底数是常数,真数是变量,从而得出对数函数的定义:一般地,我们把,且叫做对数函数,其中是自变量。函数的定义域是(0,+∞).注意:①对数函数的定义与指数函数类似,都是形式定义,注意辨别.如:,都不是对数函数.②对数函数对底数的限制:,且3.例题讲解;例1求下列函数的定义域:说明:本例主要考察对数函数定义中底数和定义域的限制,加深对概念的理解,所以可以把教材中的解答题改为填空题,节省时间,点到为止,以避免挖深、拓展、引入复合函数的概念。[设计意图:新课标强调“考虑到多数高中生的认知特点,为了有助于他们对函数概念本质的理解,不妨从学生自己的生活经历和实际问题入手”。因此,新课引入不是按旧教材从反函数出发,而是选择从学生的现实生活引出对数函数的概念,让学生熟悉它的知识背景,初步感受对数函数是刻画现实世界的又一重要数学模型。这样处理,对数函数显得不抽象,学生容易接受,降低了新课教学的起点](二)动手实践合作交流1.确定探究问题教师:当我们知道对数函数的解析式之后,紧接着需要探讨什么问题?学生1:对数函数的图象和性质教师:你能类比前面研究指数函数的思路,提出研究对数函数图象和性质的方法吗学生2:先画图象,再根据图象得出性质教师:画图的具体步骤是怎么样的?学生2:三步,列表、描点、连线教师:画对数函数的图象是否象指数函数那样也需要分类?学生3:按和分类讨论教师:观察图象主要看哪几个特征?学生4:从图象的形状、位置、升降、定点等角度去分析图像教...