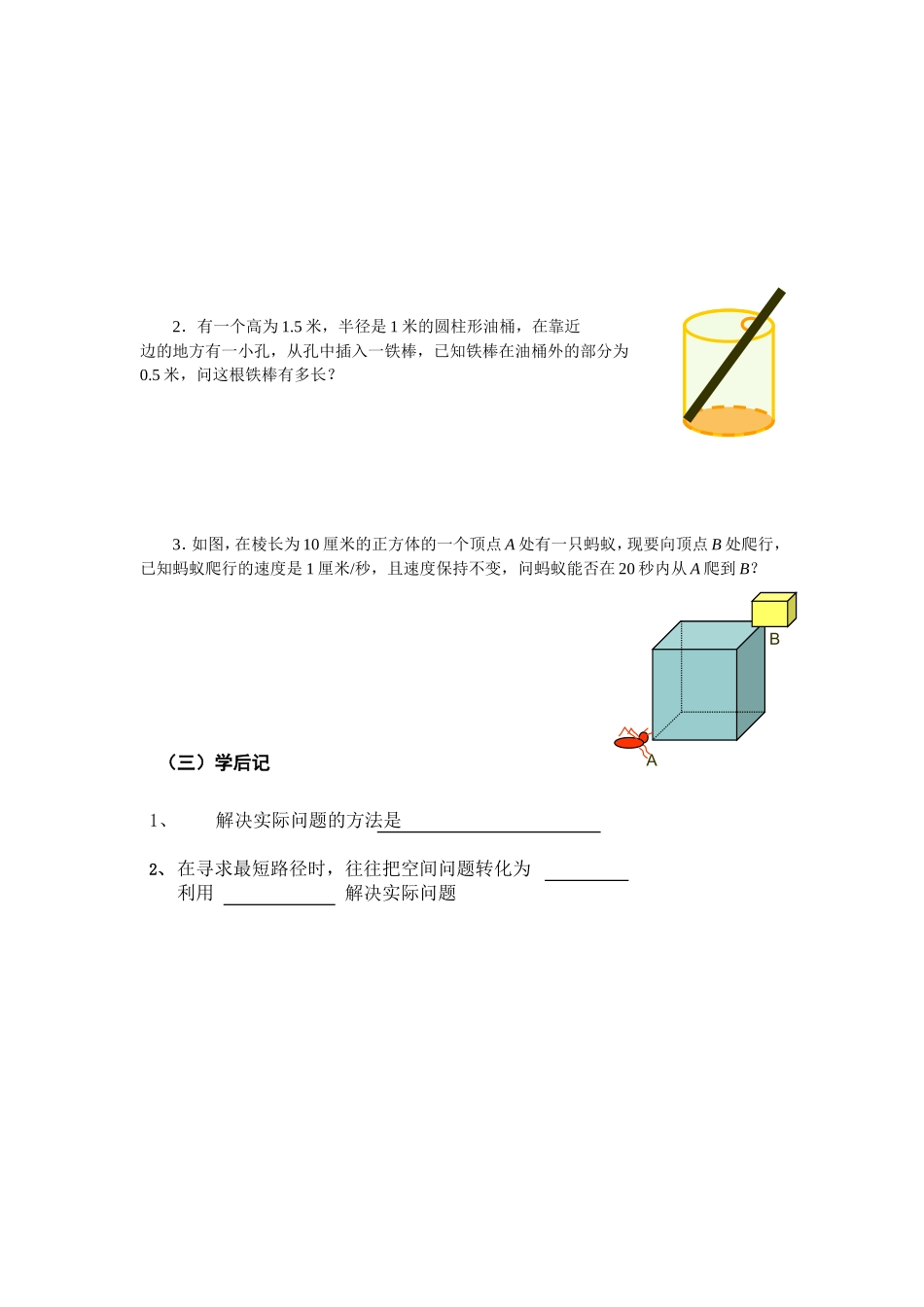
第一章勾股定理3.蚂蚁怎么走最近主备人:李翠玲一、学习目标1、学会观察图形,勇于探索图形间的关系,培养学生的空间观念.2、运用勾股定理及逆定理解决实际问题.二、教学重点探索、发现事物中隐含的勾股定理及其逆及理,并用它们解决生活实际问题.三、教学难点利用数学中的建模思想构造直角三角形,利用勾股定理及逆定理,解决实际问题.四、学习过程(一)知识准备1、在△ABC中,∠C=90°,则(勾股定理)2、在△ABC中,∠A、∠B、∠C所对的边分别是a、b、c,若a2+b2=c2则3、在平面内,两点之间最短(二)课堂探究探究一如图:在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A处爬向B处,你们想一想,沿圆柱侧面爬行的最短路程是多少?(π的值取3)(学生分为4人活动小组,合作探究蚂蚁爬行的最短路线,充分讨论后,在全班范围内展示交流。)巩固练习:在四边形ABCD中,∠B=90°,AB=4,BC=3,CD==12,AD=13,求四边形ABCD的面积探究二阅读P23做一做,完成问题(1)、(2)、(3)提示:对于问题(3)小组合作交流后,全班展示交流.拓展练习:1、如图,台阶A处的蚂蚁要爬到B处搬运食物,它怎么走最近?并求出最近距离.ABCD2.有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒有多长?3.如图,在棱长为10厘米的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是1厘米/秒,且速度保持不变,问蚂蚁能否在20秒内从A爬到B?(三)学后记1、解决实际问题的方法是2、在寻求最短路径时,往往把空间问题转化为利用解决实际问题BA