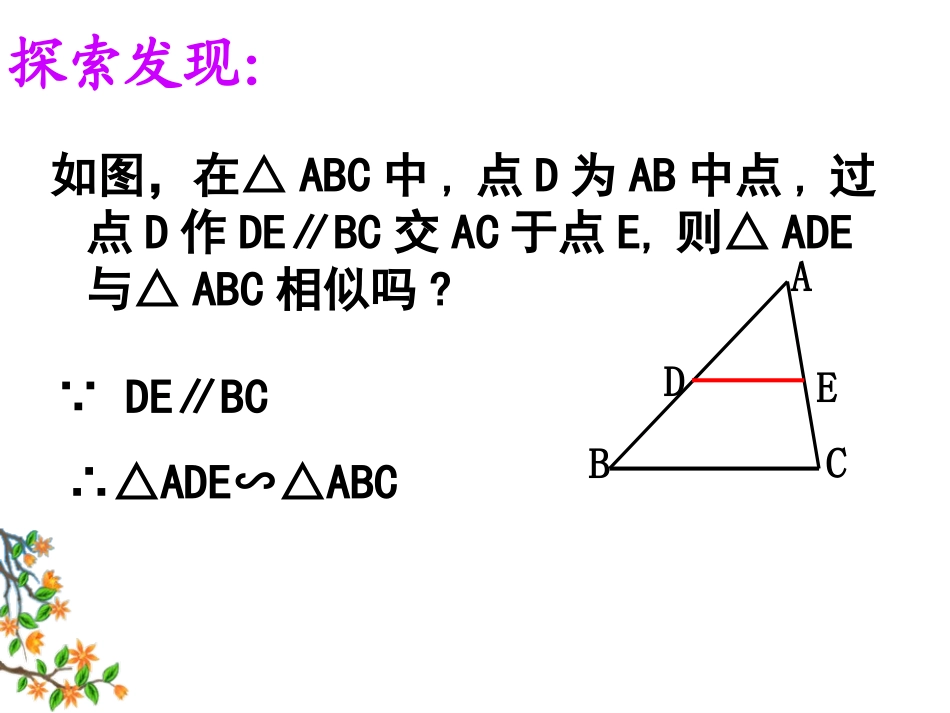
对应角相等,对应边成比例的两个三角形是相似三角形.1、相似三角形的定义:AC′B′A′CB∴△ABC△ABC´´´.ACCACBBCBAABCC,BB,AA∵∽相似三角形的判定方法:1、对应角相等,对应边成比例(定义)2、传递性如图,在△ABC中,点D为AB中点,过点D作DE∥BC交AC于点E,则△ADE与△ABC相似吗?DABCE探索发现:∵DE∥BC∴△ADE∽△ABC变式1:如图,若点D是AB边上的任意一点,过点D作DE∥BC,则△ADE与△ABC是否相似?ABCDE∵DEBC∥∴△ADE∽ABC△F变式2:若点D是BA延长线上的一点,过点D作DE∥BC,与CA的延长线交于点E,△ADE与△ABC相似吗?ABCED∵DE∥BC∴△ADE∽△ABC平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似。相似三角形判定的基本定理:DABCE∵DEBC∥∴△ADE∽ABC△(或两边的延长线)“平行截得相似”“A”型“X”型相似三角形判定方法1、对应边成比例且对应角相等;3、平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似。2、相似三角形的传递性;1、如图,已知DE∥BC,DF∥AC,请尽可能多地找出图中的相似三角形,并说明理由。ABCDFE试试眼力:三角形相三角形相似具有似具有传传递性递性!!1.DE∥BC2.DF∥ACΔADE∽ΔDBFΔADE∽ΔABCΔDBF∽ΔABC3.ΔDBF∽ΔABCΔADE∽ΔABCABCDEF2、如图,在平行四边形ABCD中,E是AB上的一点,CE和DA的延长线交于点F,找出图中相似三角形(全等三角形除外).3.如图,DEBC∥,(1)如果AD=2,DB=3,求DE:BC的值;(2)如果AD=8,DB=12,AC=15,DE=7,求AE和BC的长.4.如图,在□ABCD中,EFAB∥,DE:EA=2:3,EF=4,求CD的长.自学:P78“例1、例2”练习:P78“练习”T1、如图,点F在平行四边形ABCD的边AB的延长线上,连接DF交BC于点E.求证:ECBEABBF1、如图,在ABCD中,E是边BC上的一点,且BE:EC=3:2,连接AE、BD交于点F,则BE:AD=_____,BF:FD=_____。2、如图,在△ABC中,∠C的平分线交AB于D,过点D作DEBC∥交AC于E,若AD:DB=3:2,则EC:BC=______。ABCDEFABCED反馈练习:3:53:53:5梯形ABCD中,ABCD∥,AB=2DC,E,F为中点.求证:(1)△EDMFBM∽△;(2)BD=9,求BM的长拓展提高:相似三角形定义对应角相等对应边成比例表示法:∽相似比:(对应边的比)K≠1两个形状相同大小不等的相似三角形K=1两个全等三角形,是相似三角形特例ABCDEF如图,在平行四边形ABCD中,E是AB上的一点,CE和DA的延长线交于点F根据本节所得预备定理找出图中相似三角形(全等三角形除外).变式二:G为BC延长线上一点G小结相似三角形定义对应角相等对应边成比例表示法:∽相似比:(对应边的比)K≠1两个形状相同大小不等的相似三角形K=1两个全等三角形,是相似三角形特例预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。