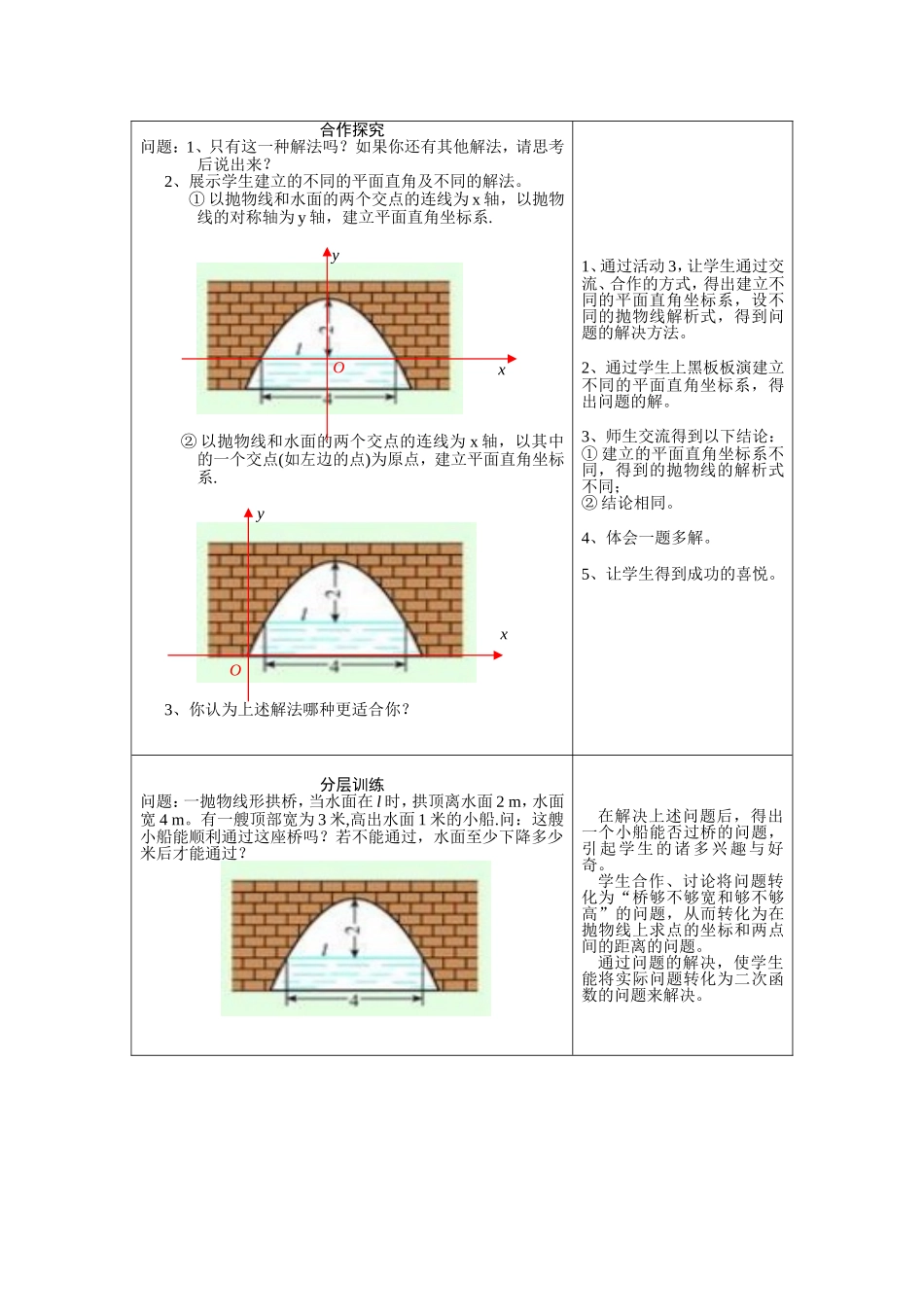
《实际问题与二次函数》教学设计教学目标:1、知识技能:通过实际问题与二次函数关系的探究,使学生经历构建平面直角坐标系解决抛物线型实际问题。2、数学思考:通过构建不同直角坐标系解决拱桥问题的探究,体会建立数学模型的思想。3、解决问题:通过解决拱桥问题的研究,体会数学知识的现实意义,进一步认识如何利用二次函数的有关知识解决实际问题。4、情感态度:通过构建不同直角坐标系解决拱桥问题,体会到解决问题方法的多样性,从而提高学生学习数学的信心和兴趣。重点、难点重点:建立平面直角坐标系,应用二次函数知识解决拱桥问题。难点:如何构建适当的平面直角坐标系解决实际问题和将实际问题转化为二次函数的问题。教学课程设计:教学流程及内容设计教学策略及意图设疑引导教师通过课件展示美丽的桥。提出下列问题:1、它们有什么共同特点?2、你能说出二次函数的不同形式表达式及其对称轴、顶点坐标吗?通过图片的欣赏,创设情境,激发学生兴趣,为新课讲解奠定基础。合作探究问题:一抛物线形拱桥,当水面在l时,拱顶离水面2m,水面宽4m.水面下降1m,水面宽度增加多少?分析:1.如果按如图方式建立平面直角坐标系,.如何设抛物线表示的二次函数?2.水面下降1m的含义是什么?3.如何求宽度增加多少?1、通过活动2的开展,师生共同探究如何建立平面直角坐标系?如何设抛物线的解析式,并通过学生的共同参与,解出抛物线的解析式。2、师生共同探究提出的问题,并通过学生的交流、合作、探究得出水面下降1米的含义以及求水面宽度的方法。3、解决问题,交流解题心得,体会成功的喜悦。xyO合作探究问题:1、只有这一种解法吗?如果你还有其他解法,请思考后说出来?2、展示学生建立的不同的平面直角及不同的解法。①以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.②以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.3、你认为上述解法哪种更适合你?1、通过活动3,让学生通过交流、合作的方式,得出建立不同的平面直角坐标系,设不同的抛物线解析式,得到问题的解决方法。2、通过学生上黑板板演建立不同的平面直角坐标系,得出问题的解。3、师生交流得到以下结论:①建立的平面直角坐标系不同,得到的抛物线的解析式不同;②结论相同。4、体会一题多解。5、让学生得到成功的喜悦。分层训练问题:一抛物线形拱桥,当水面在l时,拱顶离水面2m,水面宽4m。有一艘顶部宽为3米,高出水面1米的小船.问:这艘小船能顺利通过这座桥吗?若不能通过,水面至少下降多少米后才能通过?在解决上述问题后,得出一个小船能否过桥的问题,引起学生的诸多兴趣与好奇。学生合作、讨论将问题转化为“桥够不够宽和够不够高”的问题,从而转化为在抛物线上求点的坐标和两点间的距离的问题。通过问题的解决,使学生能将实际问题转化为二次函数的问题来解决。xxyyOO教学反思这节课我是采用PPT课件进行授课,由于课件展示,动态,直观,很容易把问题解决了,并放手让学生从不同角度去尝试建立坐标系,体会各种情况下所建立的坐标系是否有利于点的表示,激发学生学习的热情,给予学生以启迪。用二次函数知识解决实际问题是本章学习的一大难点,遇到实际问题学生往往无从下手,学生在解题过程中遇到一个新的问题该如何去联想?联想什么?怎样联想?这与课堂教学过程中老师解题方法的讲授至关重要,老师在课堂教学过程中应如何引导学生判断、分析、归类。为此我在另一个班采取了以下的教学过程,突出以学生为主体,教师只是引导学生经历分析——观察——抽象——概括——发现新知——解决新知的过程。为了让学生发现方法、领悟方法、运用方法,同时我特意给学生留有一定的思考和交流讨论的时间。通过几届学生授课的对比,我发现数学的自主学习,不能千遍一律,应针对具体内容采取灵活多变的方法。例如一些简单的计算的课堂可以先让学生自主预习,独立进行探究,完成课本上的填空,发现规律;然后小组共同归纳,总结规律,应用规律学习例题,解决问题。一些需要思维的课堂活需要探讨的课堂,我认为应该利用学案,不让...