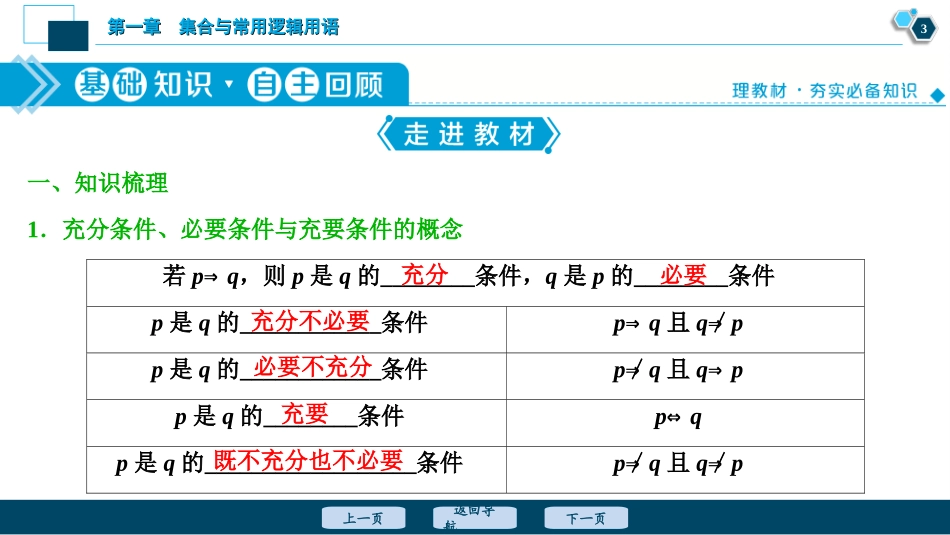
数学数学第一章集合与常用逻辑用语第一章集合与常用逻辑用语第第22讲充分条件与必要条件、全称量词讲充分条件与必要条件、全称量词与存在量词与存在量词第一章集合与常用逻辑用语第一章集合与常用逻辑用语2返回导航下一页上一页01基础知识自主回顾02学科素养探究提升03高效演练分层突破第一章集合与常用逻辑用语第一章集合与常用逻辑用语3返回导航下一页上一页一、知识梳理1.充分条件、必要条件与充要条件的概念若p⇒q,则p是q的________条件,q是p的________条件p是q的____________条件p⇒q且q⇒/pp是q的____________条件p⇒/q且q⇒pp是q的________条件p⇔qp是q的__________________条件p⇒/q且q⇒/p充分必要充分不必要必要不充分充要既不充分也不必要第一章集合与常用逻辑用语第一章集合与常用逻辑用语4返回导航下一页上一页[注意]不能将“若p,则q”与“p⇒q”混为一谈,只有“若p,则q”为真命题时,才有“p⇒q”,即“p⇒q”⇔“若p,则q”为真命题.第一章集合与常用逻辑用语第一章集合与常用逻辑用语5返回导航下一页上一页2.全称命题和特称命题(1)全称量词和存在量词量词名称常见量词符号表示全称量词所有、一切、任意、全部、每一个等______存在量词存在一个、至少有一个、有些、某些等______∀∃第一章集合与常用逻辑用语第一章集合与常用逻辑用语6返回导航下一页上一页(2)全称命题和特称命题名称形式全称命题特称命题结构对M中任意一个x,有p(x)成立存在M中的一个x0,使p(x0)成立简记__________,p(x)__________,p(x0)否定__________,﹁p(x0)__________,﹁p(x)∀x∈M∃x0∈M∃x0∈M∀x∈M第一章集合与常用逻辑用语第一章集合与常用逻辑用语7返回导航下一页上一页常用结论1.从集合的角度理解充分条件与必要条件若p以集合A的形式出现,q以集合B的形式出现,即A={x|p(x)},B={x|q(x)},则关于充分条件,必要条件又可以叙述为:(1)若A⊆B,则p是q的充分条件;(2)若A⊇B,则p是q的必要条件;(3)若A=B,则p是q的充要条件;(4)若AB,则p是q的充分不必要条件;(5)若AB,则p是q的必要不充分条件;(6)若A⊆/B且A⊉B,则p是q的既不充分也不必要条件.第一章集合与常用逻辑用语第一章集合与常用逻辑用语8返回导航下一页上一页2.全称命题与特称命题的否定(1)改写量词:确定命题所含量词的类型,省去量词的要结合命题的含义加上量词,再对量词进行改写.(2)否定结论:对原命题的结论进行否定.第一章集合与常用逻辑用语第一章集合与常用逻辑用语9返回导航下一页上一页二、教材衍化1.“(x-1)(x+2)=0”是“x=1”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:选B.若x=1,则(x-1)(x+2)=0显然成立,但反之不成立,即若(x-1)(x+2)=0,则x的值也可能为-2.故选B.2.命题“∃x0∈R,log2x0+2<0”的否定是________________________.答案:∀x∈R,log2x+2≥0第一章集合与常用逻辑用语第一章集合与常用逻辑用语10返回导航下一页上一页一、思考辨析判断正误(正确的打“√”,错误的打“×”)(1)当q是p的必要条件时,p是q的充分条件.()(2)q不是p的必要条件时,“p⇒/q”成立.()(3)写特称命题的否定时,存在量词变为全称量词.()(4)∃x0∈M,p(x0)与∀x∈M,﹁p(x)的真假性相反.()√√√√第一章集合与常用逻辑用语第一章集合与常用逻辑用语11返回导航下一页上一页二、易错纠偏常见误区(1)全称命题或特称命题的否定出错;(2)对充分必要条件判断错误.1.命题“全等三角形的面积一定都相等”的否定是__________________________.答案:存在两个全等三角形的面积不相等2.设x∈R,则“2-x≥0”是“(x-1)2≤1”的________条件.答案:必要不充分第一章集合与常用逻辑用语第一章集合与常用逻辑用语12返回导航下一页上一页考点一全称命题与特称命题(基础型)复习指导理解全称量词与存在量词的意义,能正确地对含有一个量词的命题进行否定.核心素养:数学抽象第一章集合与常用逻辑用语第一章集合与常用逻辑用语13返回导航下一页上一页1.(2020·西安模拟)命题“∀x>0,xx-1>0”的否定是()A.∃x<0,xx-1≤0B.∃x>...