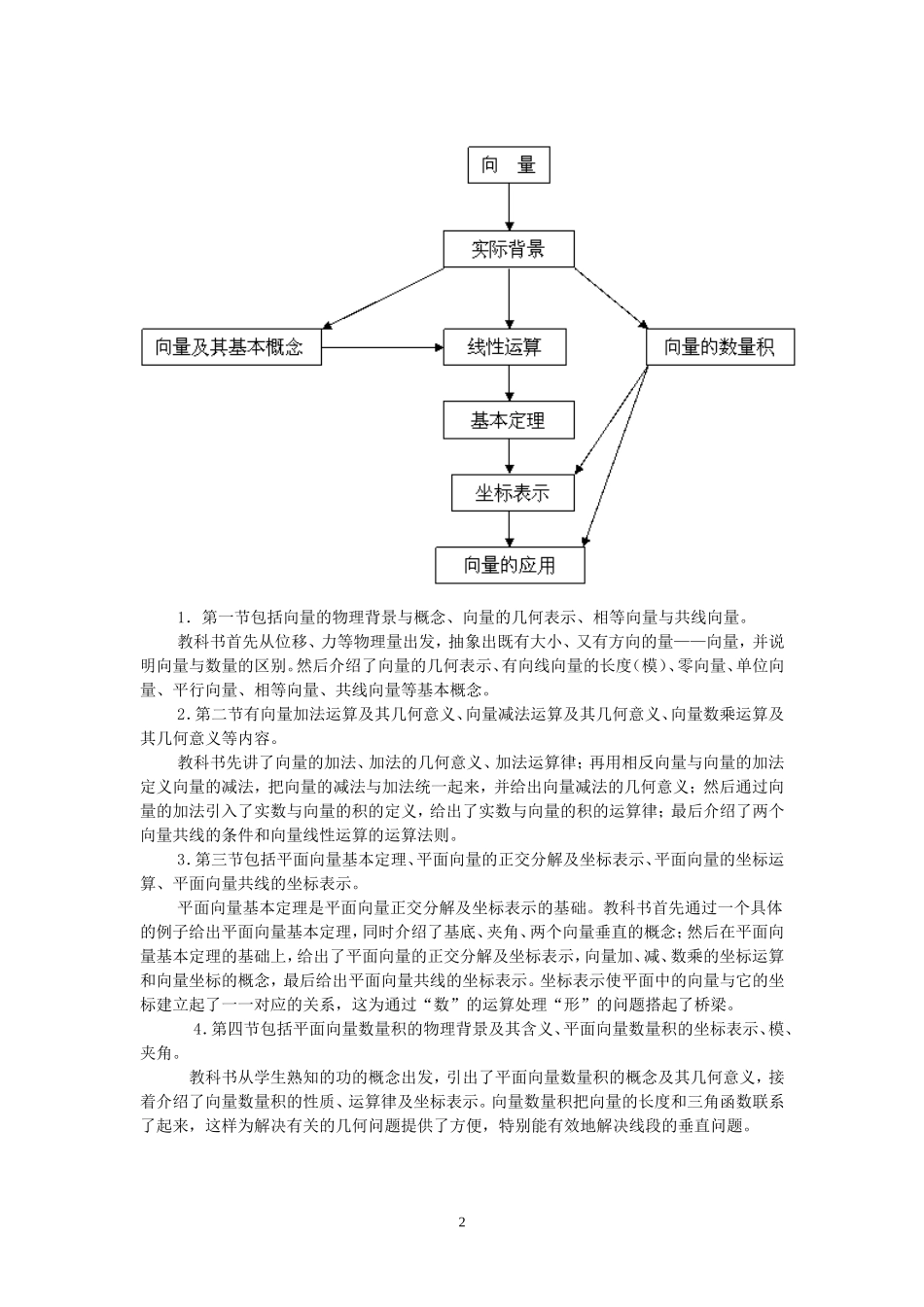
《平面向量》单元教学设计武都区两水中学王斌向量是近代数学中重要和基本的数学概念之一,有深刻的几何背景,是解决几何问题的有力工具。向量概念引入后,全等和平行(平移)、相似、垂直、勾股定理就可转化为向量的加(减)法、数乘向量、数量积运算,从而把图形的基本性质转化为向量的运算体系。向量是沟通代数、几何与三角函数的一种工具,有着极其丰富的实际背景。在本章中,学生将了解向量丰富的实际背景,理解平面向量及其运算的意义,能用向量语言和方法表述和解决数学和物理中的一些问题,发展运算能力和解决实际问题的能力。一、单元教学目标本章主要包括平面向量的实际背景及基本概念、平面向量的线性运算、平面向量的基本定理及坐标表示、平面向量的数量积、平面向量应用五部分内容。通过本章学习,应引导学生:1.通过力和力的分析等实例,知道向量的实际背景,会运用平面向量和向量相等的含义,会向量的几何表示。2.通过实例,会算向量加、减法的运算,并会求其几何意义。3.通过实例,熟练运用向量数乘的运算,并解释其几何意义,以及两个向量共线的含义。4.能说出向量的线性运算性质及其几何意义。5.知道平面向量的基本定理及其意义。6.掌握平面向量的正交分解及其坐标表示。7.会用坐标表示平面向量的加、减与数乘运算。8.解释用坐标表示的平面向量共线的条件。9.通过物理中“功”等实例,说明平面向量数量积的含义及其物理意义。10.体会平面向量的数量积与向量投影的关系。11.识记数量积的坐标表达式,会进行平面向量数量积的运算。12.能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系。13.经历用向量方法解决某些简单的平面几何问题、力学问题与其他一些实际问题的过程,体会向量是一种处理几何问题、物理问题等的工具,发展运算能力和解决实际问题的能力。二、学习者特征分析向量是近代数学中重要的和基本的概念之一,它是沟通代数几何与三角的一种工具。向量对学生来说是比较新的内容,学生对它的学习可以说是充满了探求的欲望,应当说能够使大部分学生在此章节的学习中体会到学习的成功乐趣。学生在学习本单元内容之前,已熟知了实数的运算体系,具备了物理知识.这都为学习向量准备好各方面条件.三、单元教材分析本章共安排了5个小节及2个选学内容,大约需要12个课时,具体分配如下2.1平面向量的实际背景及基本概念2课时2.2向量的线性运算2课时2.3平面向量的基本定理及坐标表示2课时2.4平面向量的数量积2课时2.5平面向量应用举例2课时小结2课时本章知识结构如下:11.第一节包括向量的物理背景与概念、向量的几何表示、相等向量与共线向量。教科书首先从位移、力等物理量出发,抽象出既有大小、又有方向的量——向量,并说明向量与数量的区别。然后介绍了向量的几何表示、有向线向量的长度(模)、零向量、单位向量、平行向量、相等向量、共线向量等基本概念。2.第二节有向量加法运算及其几何意义、向量减法运算及其几何意义、向量数乘运算及其几何意义等内容。教科书先讲了向量的加法、加法的几何意义、加法运算律;再用相反向量与向量的加法定义向量的减法,把向量的减法与加法统一起来,并给出向量减法的几何意义;然后通过向量的加法引入了实数与向量的积的定义,给出了实数与向量的积的运算律;最后介绍了两个向量共线的条件和向量线性运算的运算法则。3.第三节包括平面向量基本定理、平面向量的正交分解及坐标表示、平面向量的坐标运算、平面向量共线的坐标表示。平面向量基本定理是平面向量正交分解及坐标表示的基础。教科书首先通过一个具体的例子给出平面向量基本定理,同时介绍了基底、夹角、两个向量垂直的概念;然后在平面向量基本定理的基础上,给出了平面向量的正交分解及坐标表示,向量加、减、数乘的坐标运算和向量坐标的概念,最后给出平面向量共线的坐标表示。坐标表示使平面中的向量与它的坐标建立起了一一对应的关系,这为通过“数”的运算处理“形”的问题搭起了桥梁。4.第四节包括平面向量数量积的物理背景及其含义、平面向量数量积的坐标表示、模、夹角。教科书从学生熟知的功的概念出发,引...