等比数列课件2VIP免费

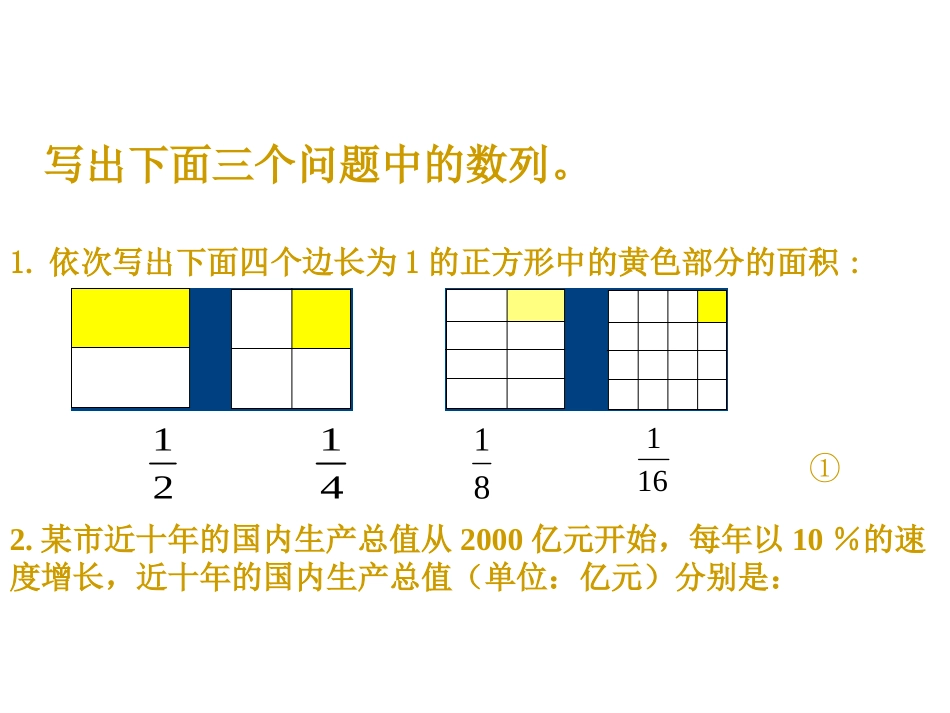
等比数列2.某市近十年的国内生产总值从2000亿元开始，每年以10％的速度增长，近十年的国内生产总值（单位：亿元）分别是：写出下面三个问题中的数列。1.依次写出下面四个边长为1的正方形中的黄色部分的面积:214181161①3.某种汽车购车时的价格是10万元，每年的折旧率是15％，这辆车各年开始的价值（单位：万元）分别是：2000，10，思考：以上三个数列有什么共同特点？2000×1.1，2000×1.12，2000×1.19。②…，10×0.85，10×0.853，10×0.852，…。③定义：一般地，如果一个数列从第二项起，每一项与它前一项的比等于同一个常数，那么这个数列就叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母q表示（q≠0）数列①②③的共同特点是：数列①②③的共同特点是：从第二项起，每从第二项起，每一项与前一项的一项与前一项的比比等于同一个常数。等于同一个常数。等比数列的定义用数学符号表示：等比数列的定义等差数列的定义是等比数列。nnnaNnnqqaa),2,0(1练习：。，，－，，－⑹。，，，，⑸。，，－，－，－－⑷。，，，－，－⑶。，，－，－，－－⑵。，，，，⑴若不是说出理由。，写出公比；是否是等比数列，若是观察以下数列，判定它1010.0101.1111.8421.8421.8141211.)21(q是，（是，q＝2）（是，q=－2）（是，q＝1）（不是）（不是）怎样推导等比数列的通项公式怎样推导等比数列的通项公式??方法一:等差推导a3=a2q=a1q2，a4=a3q=a2q2=a1q3，……由此得到an=a1qn-1已知等比数列｛an｝的首项是a1，公比是q，求an．由定义：qaann1a2=a1q，得到：方法二：1)1(1342312nnnnqqqaaaaaaaa＝个－,12qaa,23qaa)2(1nqaann,34qaa……由定义：qaann1得到：等比数列的通项公式：an=a1qn-1（nN∈﹡,q≠0）特别地，等比数列{an}中，a1≠0,q≠0等比数列的图象１（2）数列：12345678910123456789100●●●●,81,41,21,1,2,4,8●●●等比数列的图象２（1）数列：1，-1，1，-1，1，-1，1，…12345678910123456789100●●●●●●●●●●若数列{an}的首项是a1=1,公比q=2,则用通项公式表示是：＿＿＿＿＿＿an=2n－1上式还可以写成nna221可见，表示这个等比数列的各点都在函数的图象上，如右图所示。xy22101234nan87654321····图象的点函数的图象上一些孤立的图象是其对应的等比数列结论na：例题讲解分析：可由等比数列的知识求解例２见课本Ｐ５７补充练习1.等比数列｛an｝中，a1＝1，q＝－3，则a8＝____,an=__________.2.等比数列｛an｝中，a1＝2，a9＝32，则q＝____。3.一个等比数列的第9项是16，公比是－2，则它的第1项a1=_____.－37（－3）n－12161小结4.由下列等比数列的通项公式，求首项与公比：⑴an=2n；.10412nna小结解：⑴a1=2，q＝210,254101qa⑵5.已知数列x，x(1－x)，x(1－x)2，…是等比数列，则实数x的取值范围是＿＿＿A.x≠1B.x≠0，或x≠1C.x≠0D.x≠0,且x≠1D6.在等比数列中，已知首项为，末项为，公比为，则项数是＿＿＿A.3B.4C.5D.6893132B小结例３．一个等比数列的第３项和第４项分别是１２和１８，求它的第１项和第２项．(分析：要求第１项和第２项，必先求公比q.可利用方程的思想进行求解。)例３．一个等比数列的第３项和第４项分别是１２和１８，求它的第１项和第２项．解：用｛an｝表示题中公比为q的等比数列，由已知条件，有,18,1243aa18123121qaqa即解得因此，答：这个数列的第1项与第2项分别是.8316与11nnqaa练习823316qaa12316a123qn2n3n6是n）21(n)31(n)61(是结论：如果是项数相同的等比数列，那么也是等比数列．nanbnnba证明：设数列的公比为p，的公比为q，那么数列的第n项与第n+1项分别为与，即与．因为它是一个与n无关的常数，所以是一个以pq为公比的等比数列．nanbnnba1n11n1qbpan1n1qbpa1n11)pq(ban11)pq(ba,pq)pq(ba)pq(bababa1n11n11nn1n1n特别地，如果是等比数列，c是不等于０的常数，那么数列也是等比数列．nanac...