双曲线的简单几何性质（）课件-人教A版高二数学选修-VIP免费

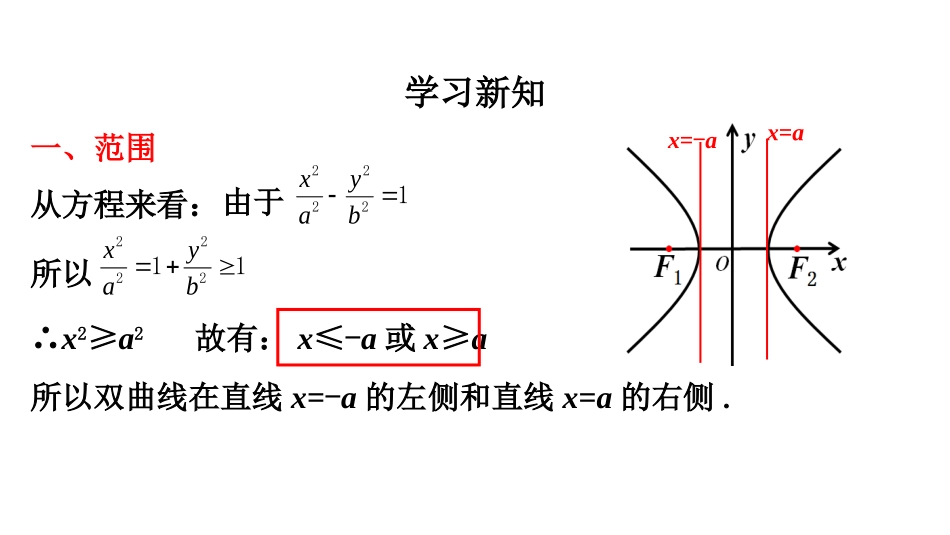
2.3.2双曲线的简单几何性质（一）平潭高中数学学科工作室杨国朱改编复习引入问题1：双曲线的定义是什么？问题2：双曲线的标准方程是什么？平面内，与两定点F1、F2的距离之差的绝对值等于常数(小于|F1F2|)的点的轨迹)00(12222b,abyax)00(12222b,abxay问题3：前面，我们研究了椭圆的哪些几何性质？范围、对称性、顶点、离心率等问题4：双曲线有哪些几何性质呢？学习新知一、范围从方程来看：∴x2≥a2所以双曲线在直线x=-a的左侧和直线x=a的右侧.12222byax由于112222byax所以故有：x≤-a或x≥ax=-ax=a学习新知二、对称性以-x代x，方程不变，所以双曲线关于y轴对称．我们把双曲线的对称中心叫做双曲线的中心.以-y代y，方程不变，所以双曲线关于x轴对称．以-x代x，以-y代y，方程不变，所以双曲线关于原点对称．)00(12222b,abyax学习新知三、顶点双曲线与x轴的交点为A1(-a，0)和A2(a，0)，它们叫做双曲线的顶点.双曲线与y轴没有交点，但我们仍把B1(0，-b)和B2(0，b)画在y轴上.线段A1A2叫做双曲线的实轴，它的长为2a，a叫做双曲线的半实轴长；)00(12222b,abyax线段B1B2叫做双曲线的虚轴，它的长为2b，b叫做双曲线的半虚轴长.xOA1yA2B1B2F2F1学习新知三、顶点实轴和虚轴等长的双曲线叫做等轴双曲线.xOA1yA2B1B2F2F1)0(222aayx焦点在x的等轴双曲线)0(222aaxy焦点在y的等轴双曲线)0(22mmyx等轴双曲线：双曲线的两支向外延伸时，与矩形的两条对角线逐渐接近，我们把这两条直线叫做双曲线的渐近线.学习新知四、渐近线如图，直线x=a和直线y=b围成了一个矩形，矩形的两条对角线的方程是什么？)00(12222b,abyaxxOA1yA2B1B2F2F1xaby等轴双曲线的渐近线：y=x（此环节根据学生情况增加已知双曲线方程求渐近线和已知渐近线求双曲线方程等）xOA1yA2B1B2F2F1学习新知五、离心率双曲线的焦距与实轴长的比，叫做双曲线的离心率.即：ace双曲线的离心率的范围：(1，+∞)>122acace222221ababa双曲线的开口大小与e的关系：e越大，开口越大等轴双曲线的离心率：2e归纳总结方程焦点顶点范围对称性中心：原点；对称轴：x轴、y轴虚实轴实轴长：2a；虚轴长：2b离心率渐近线)00(12222b,abyax)00(12222b,abxayF1(-c，0)，F2(c，0)A1(-a，0)，A2(a，0)x≤-a或x≥a)1(,aceF1(0，-c)，F2(0，c)A1(0，-a)，A2(0，a)y≤-a或y≥axabyxbay典例分析例1：求双曲线9y2-16x2=144的半实轴长和半虚轴、焦点坐标、离心率、渐近线方程.解：双曲线标准方程为：∴半实轴长a=4，半虚轴长b=3191622xy焦点为F1(0，-5)，F2(0，5)522bac离心率45ace渐近线方程：xy34课堂练习练习1：求符合下列条件的双曲线的标准方程.(1)顶点在x轴上，实轴长为6，；35e(2)焦点在y轴上，焦距为16，；34e116922yx1283622xy15522xy(3)，且过点M(-2，3).2e课堂练习练习2：(1)双曲线的渐近线方程是；12222byax(2)双曲线的渐近线方程是.)0(2222byax0byax0byax归纳总结结论：(1)双曲线与有共同渐近线.12222byax)0(2222byax0byax(2)以为渐近线的双曲线是.0byax)0(2222byax典例分析例2：求符合下列条件的双曲线的标准方程.(1)与双曲线有共同渐近线，且过点P(-3，)；32116922yx解：设所求双曲线为：16922yx则有：1612141∴双曲线方程为：144922yx典例分析例2：求符合下列条件的双曲线的标准方程.解：∴双曲线方程为：1271222xy则有：41设所求双曲线为：4922yx3(2)过点P(3，4)，渐近线为.xy32典例分析例2：求符合下列条件的双曲线的标准方程.(3)与椭圆有共同焦点，渐近线为.xy21131322yx解：c2=13-3=10104∴双曲线方程为：12822yx则有：1422yx设所求双曲线为：)0(422yx21.双曲线的几何性质（范围，对称性，顶点，离心率，渐近线）(1)由双曲线的标准方程得出双曲线的几何性质；(2)由几何性质求双曲线的标准方程，要注意先确定焦点所...