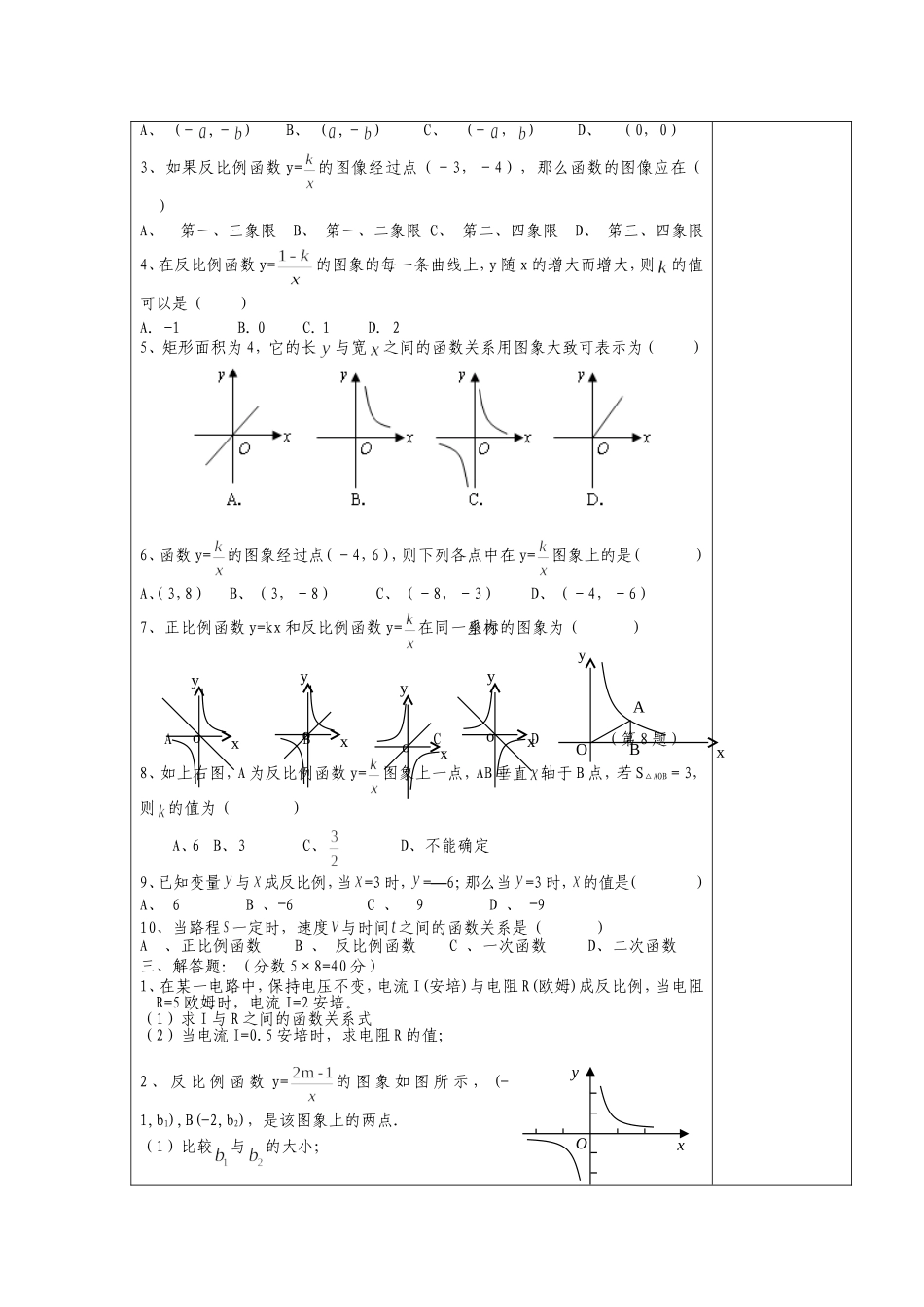
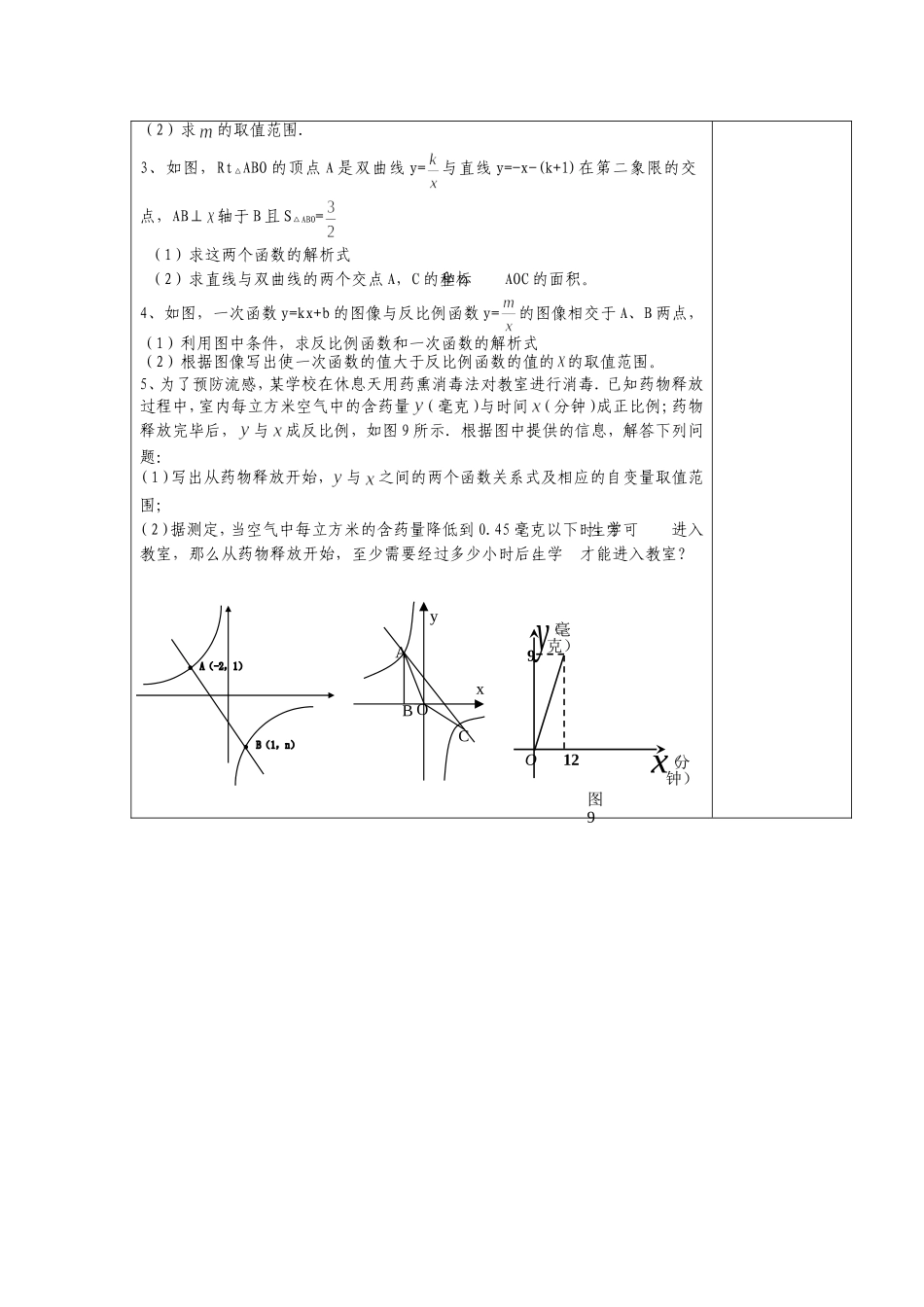
课题反比例函数测试题课型复习教学目标知识与技能通过对实际问题中数量关系得探索,掌握用函数的思想去研究其变化规律过程与方法结合具体情境体会和理解反比例函数的意义,并解决与它们有关的简单的实际问题情感与态度让学生参与知识的发现和形成过程,强化数学的应用与建模意识,提高分析问题和解决问题的能力。教学重点反比例函数的图像和性质在实际问题中的运用。教学难点运用函数的性质和图像解综合题,要善于识别图形,勤于思考,获取有用的信息,灵活的运用数学思想方法。教具准备教学过程教师活动学生活动一、填空题:(分数3分×10=30分,)1、与成反比,且当=6时,t=,这个函数解析式为;2、函数y=和函数y=的图像有个交点;3、反比例函数y=的图像经过(-,5)点、(,-3)及(10,)点,则=,=,=;4、若函数y=(4m-1)xm-4是正比例函数,那么m=,图象经过象限;5、请你写出一个图象在第一、三象限的反比例函数.答:.6、设有反比例函数y=,y随x的增大而减小,则的取值范围是___________7、右图3是反比例函数y=的图象,则k与0的大小关系是k0.8、函数y=的图像,在每一个象限内,随的增大而;9、反比例函数y=在第一象限内的图象如图,点M是图像上一点,MP垂直轴于点P,如果△MOP的面积为1,那么的值是;10、y=(m2-1)是关于的反比例函数,则的值为;二、选择题:(分数3分×10=30分,)1、点(13)P,在反比例函数y=的图象上,则k的值是().A.13B.3C.D.32、已知反比例函数的图像经过点(,),则它的图像一定也经过()yxOPMA、(-,-)B、(,-)C、(-,)D、(0,0)3、如果反比例函数y=的图像经过点(-3,-4),那么函数的图像应在()A、第一、三象限B、第一、二象限C、第二、四象限D、第三、四象限4、在反比例函数y=的图象的每一条曲线上,y随x的增大而增大,则的值可以是()A.-1B.0C.1D.25、矩形面积为4,它的长与宽之间的函数关系用图象大致可表示为()6、函数y=的图象经过点(-4,6),则下列各点中在y=图象上的是()A、(3,8)B、(3,-8)C、(-8,-3)D、(-4,-6)7、正比例函数y=kx和反比例函数y=在同一坐标系内的图象为()ABCD(第8题)8、如上右图,A为反比例函数y=图象上一点,AB垂直轴于B点,若S△AOB=3,则的值为()A、6B、3C、D、不能确定9、已知变量与成反比例,当=3时,=6―;那么当=3时,的值是()A、6B、―6C、9D、―910、当路程一定时,速度与时间之间的函数关系是()A、正比例函数B、反比例函数C、一次函数D、二次函数三、解答题:(分数5×8=40分)1、在某一电路中,保持电压不变,电流I(安培)与电阻R(欧姆)成反比例,当电阻R=5欧姆时,电流I=2安培。(1)求I与R之间的函数关系式(2)当电流I=0.5安培时,求电阻R的值;2、反比例函数y=的图象如图所示,(-1,b1),B(-2,b2),是该图象上的两点.(1)比较与的大小;yxoyxoyxoyxoABOxyyxO(2)求的取值范围.3、如图,Rt△ABO的顶点A是双曲线y=与直线y=-x-(k+1)在第二象限的交点,AB⊥轴于B且S△ABO=(1)求这两个函数的解析式(2)求直线与双曲线的两个交点A,C的坐标和△AOC的面积。4、如图,一次函数y=kx+b的图像与反比例函数y=的图像相交于A、B两点,(1)利用图中条件,求反比例函数和一次函数的解析式(2)根据图像写出使一次函数的值大于反比例函数的值的的取值范围。5、为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量(毫克)与时间(分钟)成正比例;药物释放完毕后,与成反比例,如图9所示.根据图中提供的信息,解答下列问题:(1)写出从药物释放开始,与之间的两个函数关系式及相应的自变量取值范围;(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?OyxBACO9(毫克)12(分钟)xy图9