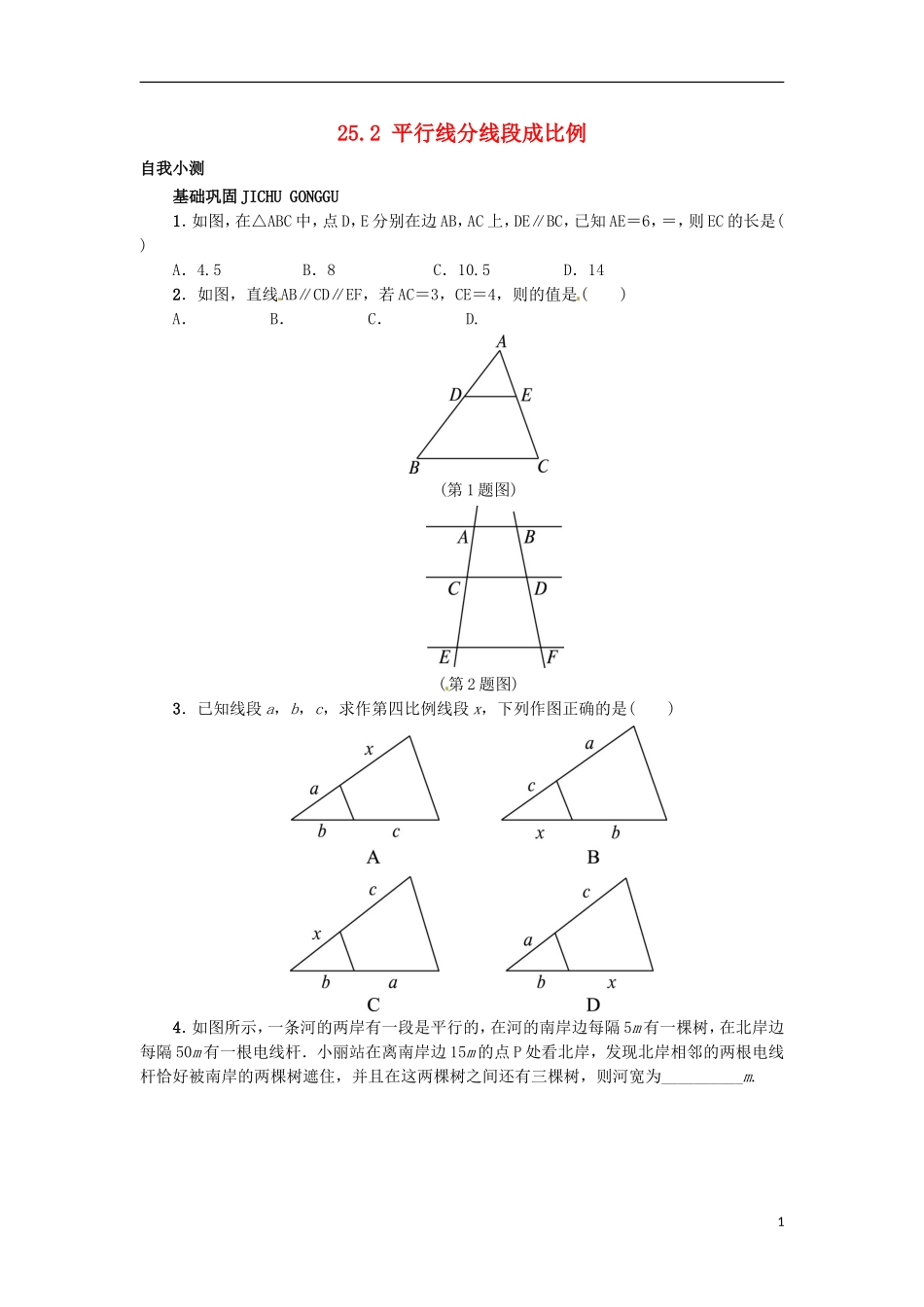
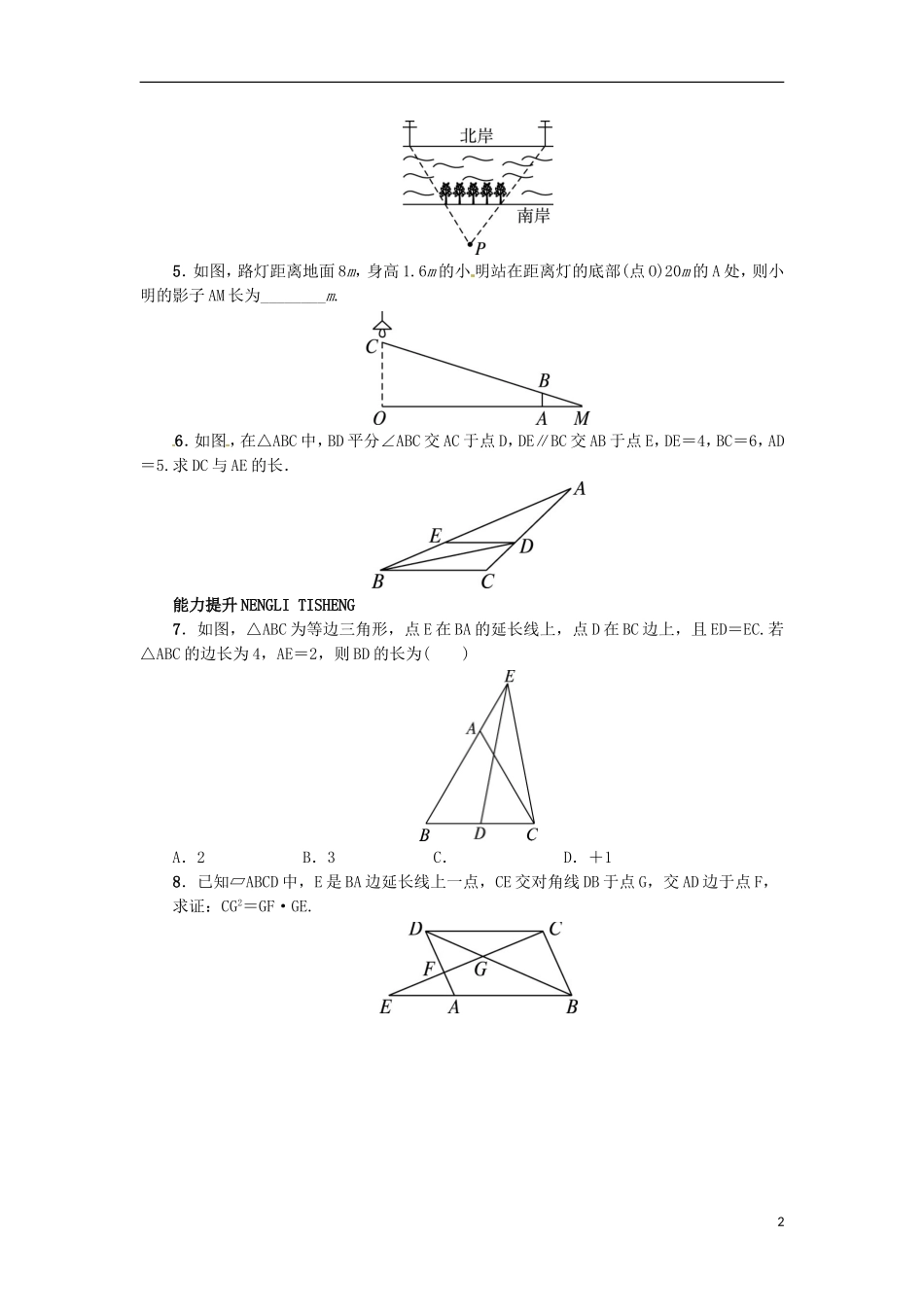
25.2平行线分线段成比例自我小测基础巩固JICHUGONGGU1.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,=,则EC的长是()A.4.5B.8C.10.5D.142.如图,直线AB∥CD∥EF,若AC=3,CE=4,则的值是()A.B.C.D.(第1题图)(第2题图)3.已知线段a,b,c,求作第四比例线段x,下列作图正确的是()4.如图所示,一条河的两岸有一段是平行的,在河的南岸边每隔5m有一棵树,在北岸边每隔50m有一根电线杆.小丽站在离南岸边15m的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为__________m.15.如图,路灯距离地面8m,身高1.6m的小明站在距离灯的底部(点O)20m的A处,则小明的影子AM长为________m.6.如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥BC交AB于点E,DE=4,BC=6,AD=5.求DC与AE的长.能力提升NENGLITISHENG7.如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC.若△ABC的边长为4,AE=2,则BD的长为()A.2B.3C.D.+18.已知▱ABCD中,E是BA边延长线上一点,CE交对角线DB于点G,交AD边于点F,求证:CG2=GF·GE.2参考答案1.B点拨:根据平行线分线段成比例的基本事实列式进行计算即可得解.2.C点拨:已知直线AB∥CD∥EF,根据平行线分线段成比例的基本事实列出比例式即可求解.3.D点拨:本题运用排除法解答,根据第四比例线段的定义列出比例式,再根据平行线分线段成比例定理对各选项图形列出比例式即可得解.∵线段x为线段a,b,c的第四比例线段,∴=.A选项,作出的为=,故本选项错误;B、C选项,线段x无法先作出,故本选项错误;D选项,作出的为=,故本选项正确.4.22.5点拨:根据题意,河两岸平行,故可根据平行线分线段成比例来解决问题,列出方程,求解即可.5.5点拨:根据题意,易知AB∥OC,则=,可得=,即=,解得AM=5.故小明的影长为5m.6.分析:根据平行线分线段成比例,可得=,求出AC,从而得到DC的长.根据等腰三角形的性质得到DE=BE=4,再由平行线分线段成比例,可得==,得到AE的长.解:∵DE∥BC,∴=.又DE=4,BC=6,AD=5,∴=.∴AC=.∴DC=AC-AD=.∵DE∥BC,∴=.∴∠DBC=∠EDB.∵BD平分∠ABC,∴∠EBD=∠DBC.∴∠EBD=∠EDB.∴DE=BE=4,==.∴AE=8.7.A点拨:延长BC至F点,使得CF=BD,∵ED=EC,∴∠EDC=∠ECD.∴∠EDB=∠ECF.在△EBD和△EFC中,∴△EBD≌△EFC(SAS).∴∠B=∠F.∵△ABC是等边三角形,∴∠B=∠ACB.∴∠ACB=∠F.∴AC∥EF.∴=.∵BA=BC,∴CF=AE=2.∴BD=CF=2.38.证明:∵四边形ABCD是平行四边形,∴DC∥AB,AD∥BC.∵DC∥AB,∴=.∵AD∥BC,∴=.∴=,即CG2=GF·GE.4