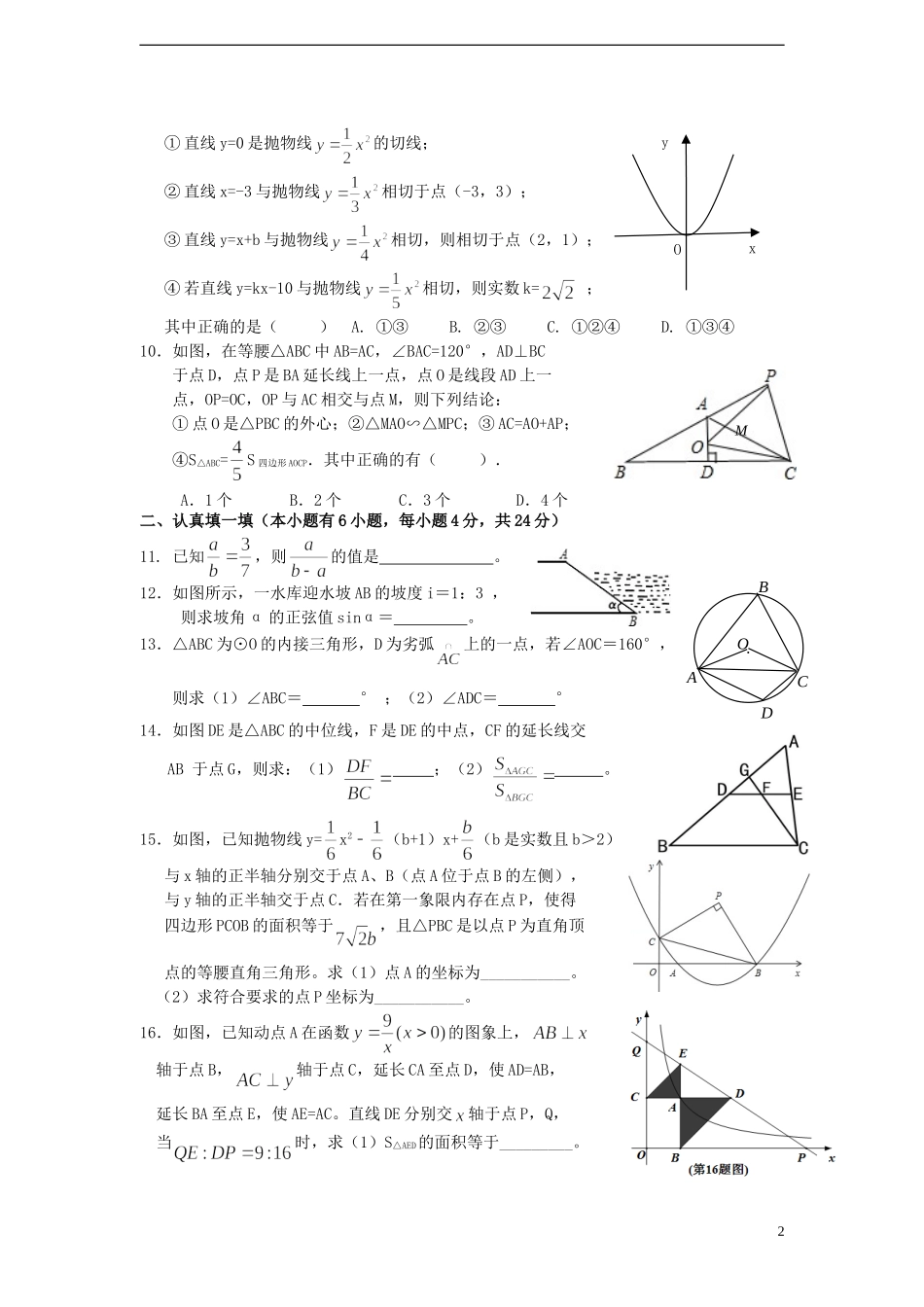
竹竿杭州市金山初中2012-2013学年第二学期九年级学习质量检测数学试卷一.仔细选一选(本题有10个小题,每小题3分,共30分)1.如图是我们已学过的某种函数图象,它的函数解析式可能是()A.B.C.D.2.若a=tan60°,b=cos60°,则它们之间的大小关系是()A.a<bB.b<aC.a=bD.无法比较3.如图,小李用长为4m的竹竿做测量工具测量学校旗杆的高度,竹移动竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为()A.11mB.15mC.30mD.60m4.如图,已知一个圆锥的高为8cm,底面圆的直径为12cm,则求这个圆锥的侧面积等于()A.B.C.D.5.在平面直角坐标系中,将抛物线向上(下)或向左(右)平移了m个单位,使平移后的抛物线恰好经过原点,则的最小值为()A.2B.4C.6D.86.在下列函数中y随x增大而增大的有()①②③(x>0)④A.①②④B.②④C.③④D.③7.如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(8,4).将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数解析式是()A.B.C.D.8.如图,△ABC是⊙O的内接三角形,AD⊥BC于D点,且AC=13,CD=5,,则⊙O的直径等于()A.12B.C.D.9.给出定义:设一条直线与一条抛物线只有一个公共点,且这条直线与这条抛物线的对称轴不平行,就称直线与抛物线相切,这条直线是抛物线的切线.有下列命题:1MBACO·D①直线y=0是抛物线的切线;②直线x=-3与抛物线相切于点(-3,3);③直线y=x+b与抛物线相切,则相切于点(2,1);④若直线y=kx-10与抛物线相切,则实数k=;其中正确的是()A.①③B.②③C.①②④D.①③④10.如图,在等腰△ABC中AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,OP与AC相交与点M,则下列结论:①点O是△PBC的外心;②△MAO∽△MPC;③AC=AO+AP;④S△ABC=S四边形AOCP.其中正确的有().A.1个B.2个C.3个D.4个二、认真填一填(本小题有6小题,每小题4分,共24分)11.已知,则的值是。12.如图所示,一水库迎水坡AB的坡度i=1:3,则求坡角α的正弦值sinα=。13.△ABC为⊙O的内接三角形,D为劣弧上的一点,若∠AOC=160°,则求(1)∠ABC=°;(2)∠ADC=°14.如图DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则求:(1);(2)。15.如图,已知抛物线y=x2﹣(b+1)x+(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.若在第一象限内存在点P,使得四边形PCOB的面积等于,且△PBC是以点P为直角顶点的等腰直角三角形。求(1)点A的坐标为___________。(2)求符合要求的点P坐标为___________。16.如图,已知动点A在函数的图象上,轴于点B,轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC。直线DE分别交轴于点P,Q,当时,求(1)S△AED的面积等于_________。2xyO(2)阴影部分的面积等于_____________。三.全面答一答(本题有7个小题,共66分)17.(本小题满分6分)如图所示,直线l1的解析式为y=-x+1,直线l2的解析式为y=x+5,且两直线相交于点P,过点P的双曲线,与直线l1的另一交点为Q(m,-2).(1)求双曲线的解析式和m的值。(2)根据图象直接写出不等式>-x+1的解集。18.(本小题满分8分)如图,△ABC三个顶点坐标分别为A(1,2)、B(3,1)、C(2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.(1)在图中第一象限内画出符合要求的△A′B′C′;(不要求写画法)(2)求△A′B′C′的面积是多少。19.(本小题满分8分)校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.(参考数据:,)(1)求AB的长(精确到0.1米),(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,问这辆校车是否超速?...