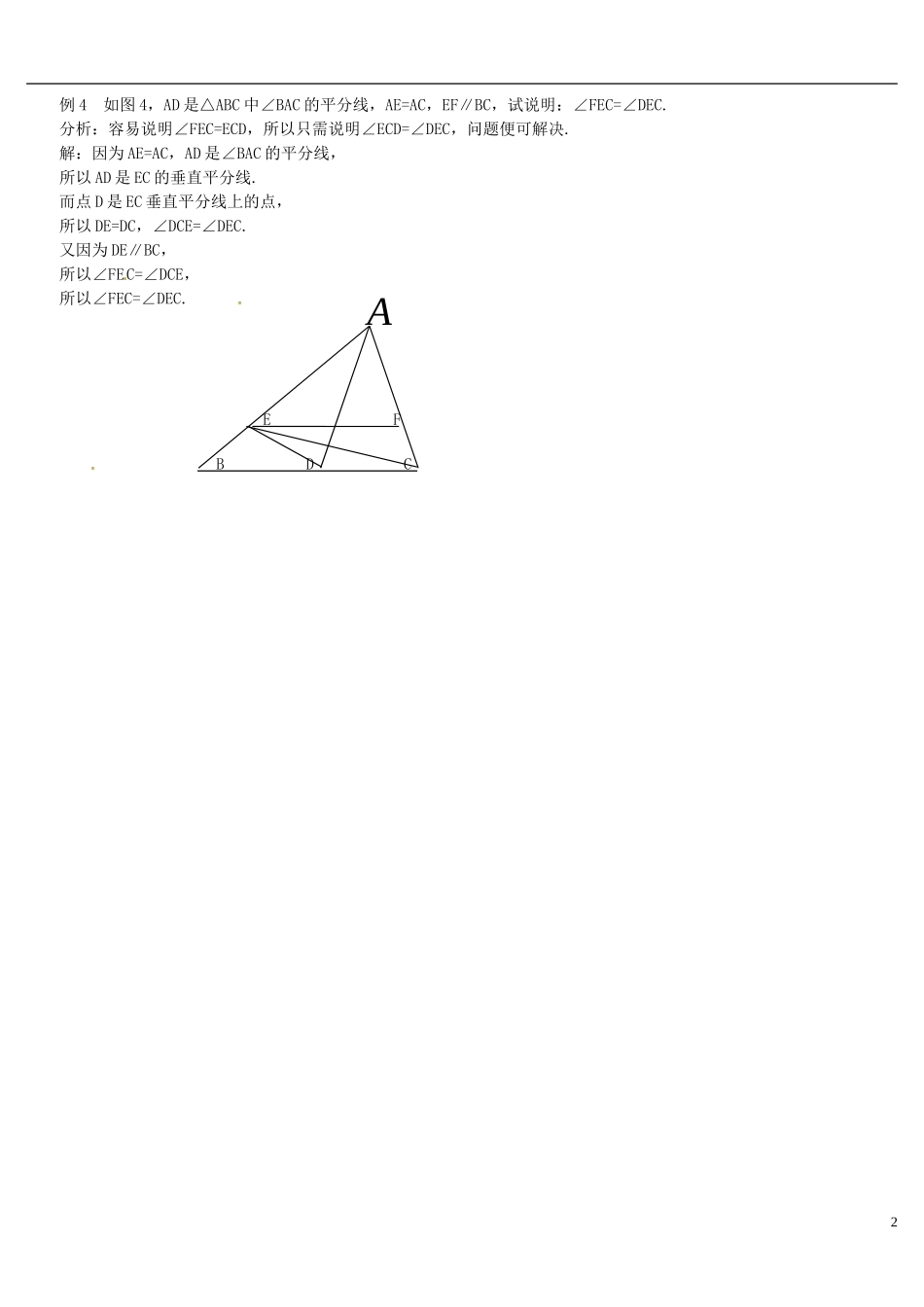
线段垂直平分线性质的应用我们知道.垂直且平分一条线段的直线是这条线段的垂直平分线,它具有如下重要的性质:线段垂直平分线上的点到这条线段两个端点的距离相等.灵活应用这个性质,可以帮助我们解决各种不同类型的题目.一、求角度例1如图1,DE是△ABC的AB边的垂直平分线,分别交AB、BC于点D、E,AE平分∠BAC,若∠B=30°,求∠C的度数.分析:因为DE是AB的垂直平分线,所以∠1=∠B.解:因为DE是AB的垂直平分线,所以EA=EB.A所以∠1=∠B=30°.又因为AE平分∠BAC,D所以∠2=∠1=30°.所以∠C=180°―∠B―∠BAC=90°.EC二、求线段的长例2如图2,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交AC于点E,△ABC的周长等于18cm,则AC的长等于()A、6cmB、8cmC、10cmD、12cm分析:因为DE是AB的垂直平分线,所以EA=EB,可以把BE+EC转化为AC.解:因为DE是AB的垂直平分线,所以EA=EB.所以AC=AE+EC=EB+EC.A又因为EB+EC+BC=18,BC=8,所以EB+EC=18-8=10.D即AC=10.E故应选C.BC三、说明线段相等例3如图3,点D、E在△ABC的边BC上,BD=CE,AB=AC,试说明:AD=AE.ABDFEC分析:由AB=AC,易联想到过点A作AF⊥BC于点F,则可说明AF是DE的垂直平分线,问题便可解决.解:过点A作AF⊥BC于点F,因为AB=AC,AF⊥BC,所以BF=CF.所以BF-BD=CF-CE,即DF=EF.所以AF是DE的垂直平分线,所以AD=AE.四、说明角相等1B例4如图4,AD是△ABC中∠BAC的平分线,AE=AC,EF∥BC,试说明:∠FEC=∠DEC.分析:容易说明∠FEC=ECD,所以只需说明∠ECD=∠DEC,问题便可解决.解:因为AE=AC,AD是∠BAC的平分线,所以AD是EC的垂直平分线.而点D是EC垂直平分线上的点,所以DE=DC,∠DCE=∠DEC.又因为DE∥BC,所以∠FEC=∠DCE,所以∠FEC=∠DEC.EFBDC2A