2015秋八年级数学上册第12章全等三角形证明题新版新人教版VIP免费

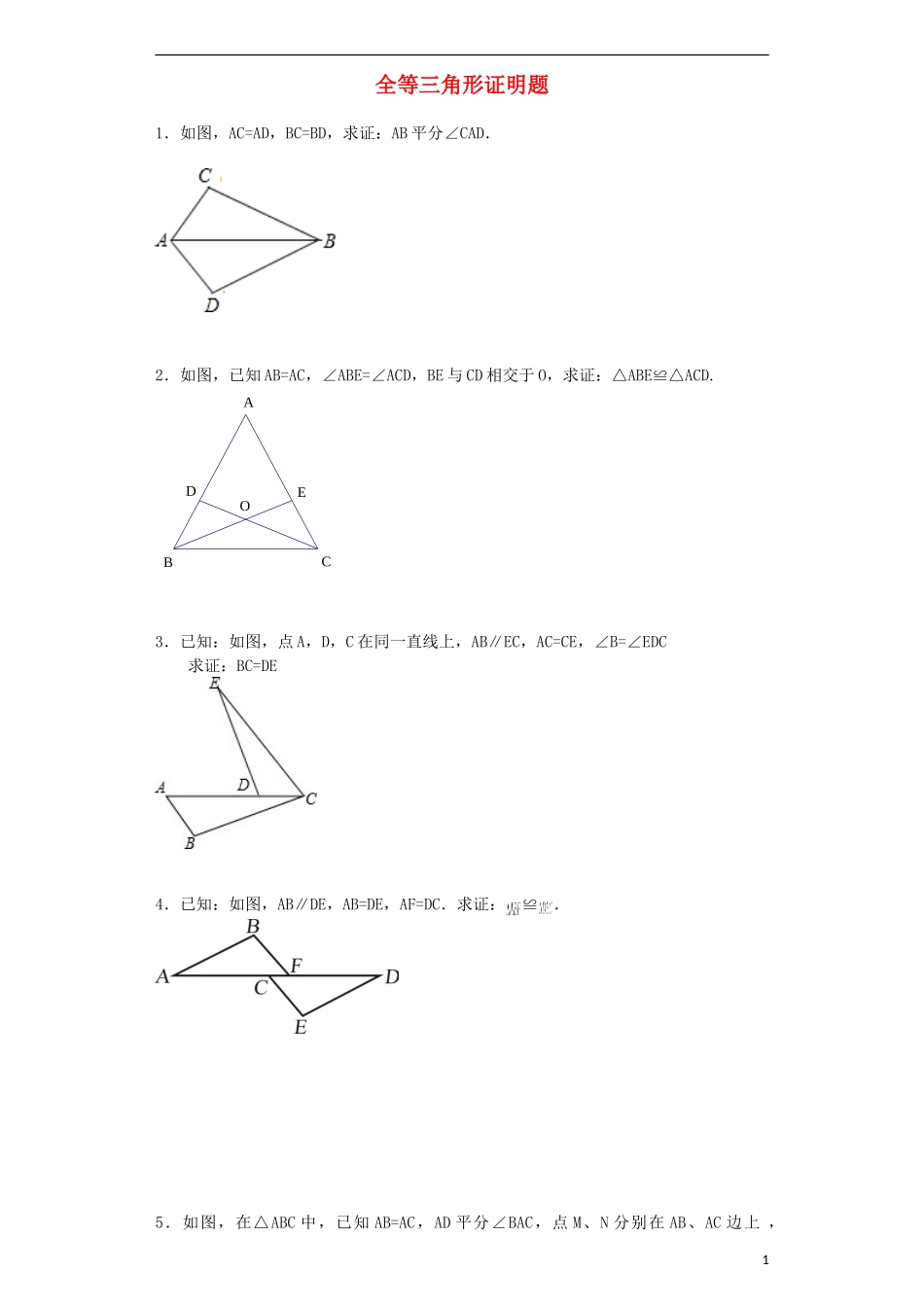
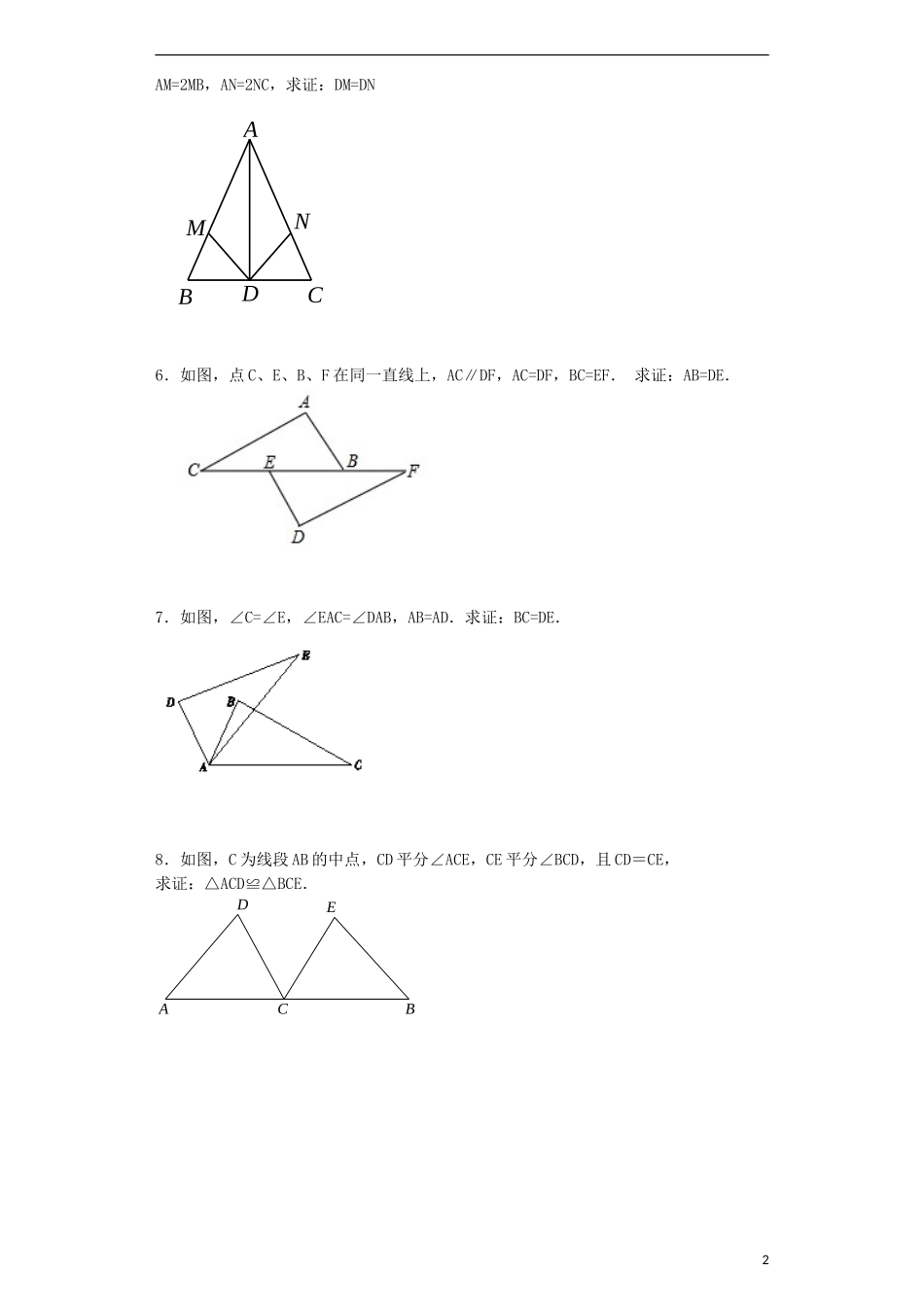
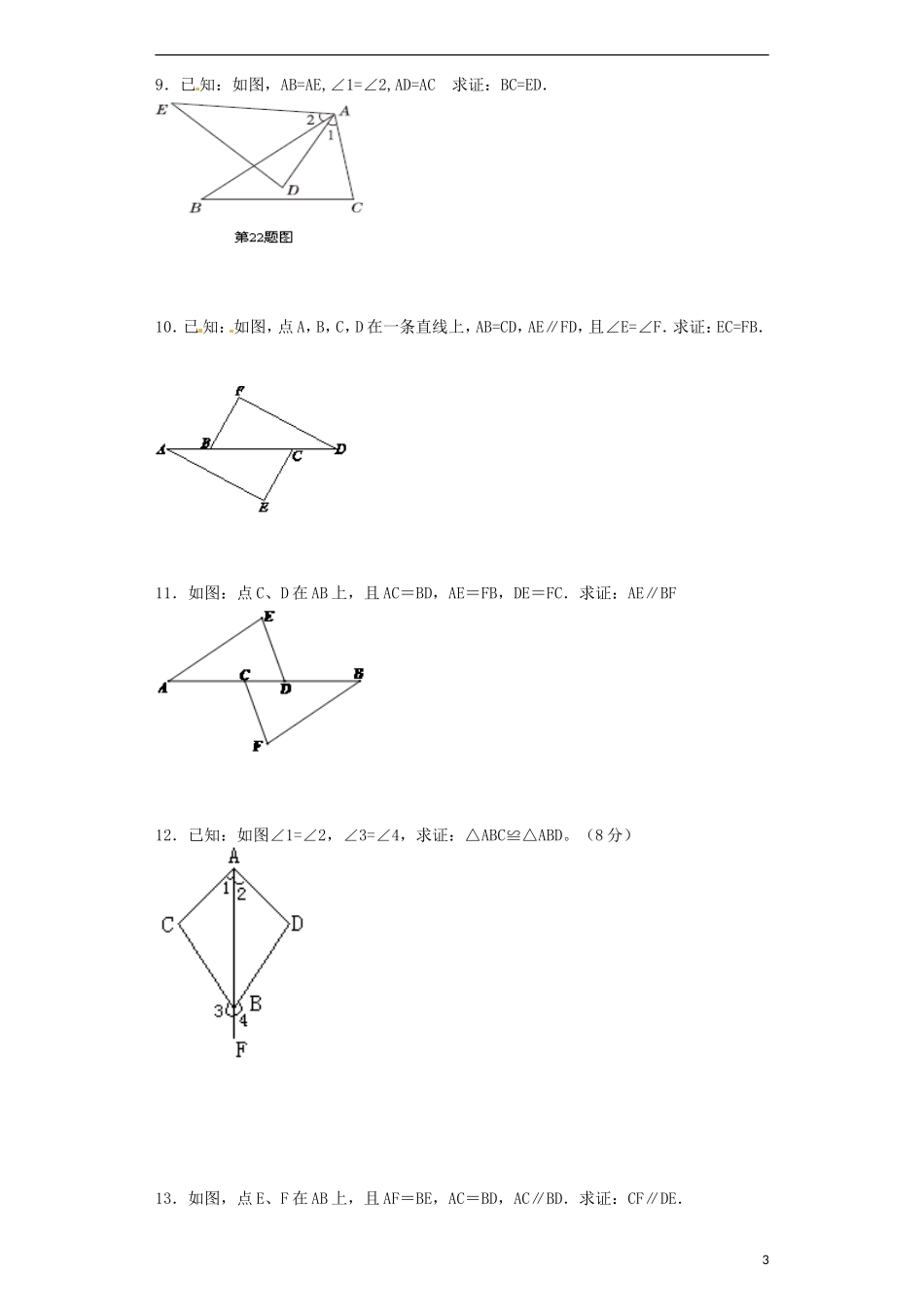
全等三角形证明题1．如图，AC=AD，BC=BD，求证：AB平分∠CAD．2．如图，已知AB=AC，∠ABE=∠ACD，BE与CD相交于O，求证：△ABE≌△ACD.3．已知：如图，点A，D，C在同一直线上，AB∥EC，AC=CE，∠B=∠EDC求证：BC=DE4．已知：如图，AB∥DE，AB=DE，AF=DC．求证：≌．5．如图，在△ABC中，已知AB=AC，AD平分∠BAC，点M、N分别在AB、AC边上，1EODCBAAM=2MB，AN=2NC，求证：DM=DN6．如图，点C、E、B、F在同一直线上，AC∥DF，AC=DF，BC=EF．求证：AB=DE．7．如图，∠C=∠E，∠EAC=∠DAB，AB=AD．求证：BC=DE．8．如图，C为线段AB的中点，CD平分∠ACE，CE平分∠BCD，且CD＝CE，求证：△ACD≌△BCE．2CDBNMAACBDE9．已知：如图，AB=AE,∠1=∠2,AD=AC求证：BC=ED．10．已知：如图，点A，B，C，D在一条直线上，AB=CD，AE∥FD，且∠E=∠F．求证：EC=FB．11．如图：点C、D在AB上，且AC＝BD，AE＝FB，DE＝FC．求证：AE∥BF12．已知：如图∠1=∠2，∠3=∠4，求证：△ABC≌△ABD。（8分）13．如图，点E、F在AB上，且AF＝BE，AC＝BD，AC∥BD．求证：CF∥DE．314．如图，点B,E,C,F在一条直线上，AB=DE,AC=DF,BE=CF,求证：∠A=∠D15．如图，在△ABC中，∠ACB=90º，D是AC上的一点，且AD=BC，DEAC于D，∠EAB=90º．求证：AB=AE．16．如图，△ABC中，AB=AC，BD⊥AC，CE⊥AB．求证：BD=CE．4FEDCBA参考答案1．证明见解析.【解析】试题分析：由已知两对边相等，加上公共边AB=AB，利用SSS得到三角形ABC与三角形ABD全等，利用全等三角形对应角相等得到∠CAB=∠DAB，即可得证．试题解析：在△ABC与△ABD中，，∴△ABC≌△ABD（SSS），∴∠CAB=∠DAB，∴AB平分∠CAD．考点：全等三角形的判定与性质．2．证明见解析.【解析】试题分析：本题比较简单，三角形全等条件中三个元素都具备，并且一定有一组对应边相等，可用“SAS”．试题解析：在△ABE与△ACD中．，∴△ABE≌△ACD（SAS）．考点：1.等腰三角形的性质；2.全等三角形的判定．3．证明见解析.【解析】试题分析：根据由两个角和其中一角的对边相等的两个三角形全等证明△ABC≌△CDE，由全等三角形的性质即可得到BC=DE． AB∥EC，∴∠A=∠DCE，在△ABC和△CDE中， ∠B＝∠EDC，∠A＝∠DCE，AC＝CE，∴△ABC≌△CDE（AAS）.∴BC=DE．考点：全等三角形的判定和性质．4．详见解析．【解析】试题分析：由AB∥DE可得∠A=∠D，又因AB=DE，AF=DC，利用“SAS”可得≌DEC．试题解析：证明： AB∥DE∴∠A=∠D AB=DE，AF=DC∴ABF≌DEC考点：平行线的性质；三角形全等的判定．5．见解析．【解析】试题分析：根据AM=2MB，AN=2NC，AB=AC得出AM=AN，根据角平分线得出∠MAD=∠NAD，结合AD=AD得出△AMD和△AND全等，从而得出MD=ND．试题解析： AM=2MB∴AM=23AB同理AN=23AC又 AB=AC∴AM=AN AD平分∠BAC∴∠MAD=∠NAD又 AD=AD∴△AMD≌△AND∴DM=DN考点：三角形全等的性质．6．证明见解析．【解析】试题分析：证明AB=DE，可以通过全等三角形来求得．三角形ABC和DEF中，已知的条件有：AC=DF，BC=EF，只要再证得两对应边的夹角相等即可得出全等的结论．试题解析：证明： AC∥DF，∴∠C=∠F．在△ACB和△DFE中ACDFCFBCEF＝＝，＝∴△ACB≌△DFE（SAS）．∴AB=DE．考点：全等三角形的判定与性质．7．证明见试题解析．【解析】试题分析：由∠EAC=∠DAB，得到∠BAC=∠DAE．即可证明△ABC≌△ADE，从而有BC=DE．试题解析：证明：如图1． ∠EAC=∠DAB，∴∠EAC+∠1=∠DAB+∠1，即∠BAC=∠DAE．在△ABC和△ADE中， CEBACDAEABAD，∴△ABC≌△ADE，∴BC=DE．考点：全等三角形的判定与性质．8．见解析【解析】试题分析：根据C为线段AB的中点，得AC=BC,由CD平分∠ACE，CE平分∠BCD，可得∠ACD=∠BCE,CD＝CE,由SAS可证△ACD≌△BCE．试题解析：因为C为线段AB的中点，所以AC=BC,又因为CD平分∠ACE，CE平分∠BCD，所以∠ACD=∠DCE,∠ECD=∠BCE,所以∠ACD=∠BCE,又CD＝CE,所以△ACD≌△BCE（SAS）．考点：全等三角形的判定．9．详见解析【解析】试题分析： ∠1=∠2，∴∠1+∠DAC=∠2+∠DAC，即：∠CAB=∠EAD，在△ACB和△ADE中：∴...