二次函数yaxbxc的图象和性质VIP免费

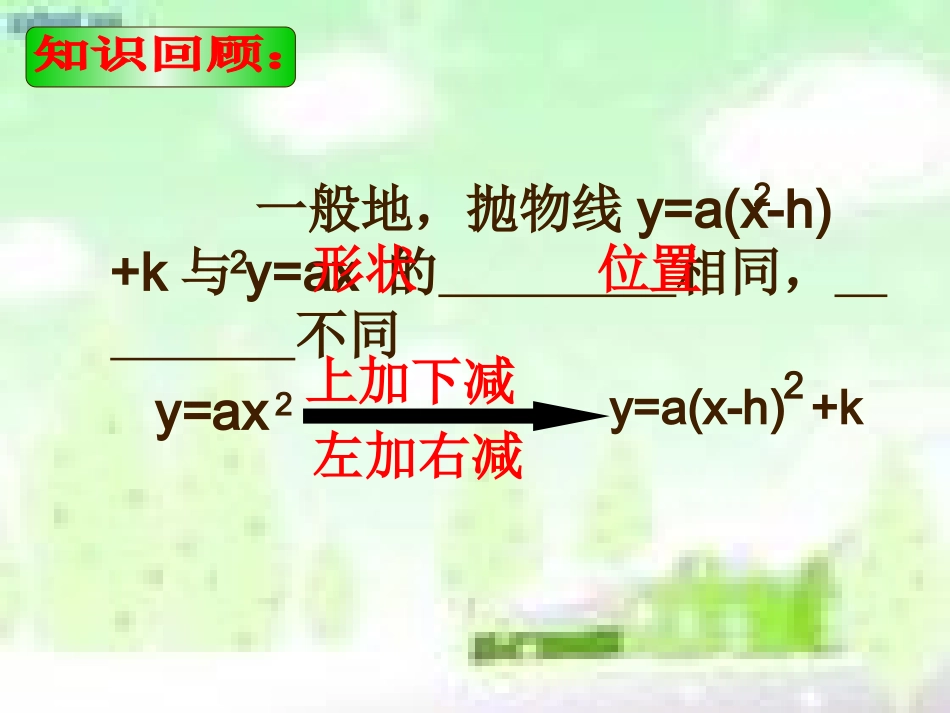
26.1.4二次函数y=ax2+bx+c的图象和性质（1）xyo沾益区炎方一中高广早一般地，抛物线y=a(x-h)+k与y=ax的相同，不同22形状位置y=ax2y=a(x-h)+k2上加下减左加右减抛物线y=a(x-h)2+k有如下特点:1.当a0﹥时，开口，当a0﹤时，开口，向上向下2.对称轴是；3.顶点坐标是。直线X=h(h,k)如何画出的图象呢?216212xxy我们知道,像y=a(x-h)2+k这样的函数,容易确定相应抛物线的顶点为(h,k),二次函数也能化成这样的形式吗？216212xxy怎样把函数转化成y=a(x-h）2+k的形式?用配方法216212xxy配方216212xxyy=—(x―6)+3212你知道是怎样配方的吗？(1)“提”：提出二次项系数；(2)“配”：括号内配成完全平方；(3)“化”：化成顶点式。配方后的表达式通常称为配方式或顶点式216212xxy4212212xx提取二次项系数42363612212xx配方66212x整理.36212x化简:去掉中括号解：根据顶点式确定开口方向,对称轴,顶点坐标.x…3456789………36212xy列表:利用图象的对称性,选取适当值列表计算.…7.553.533.557.5… a=>0,∴开口向上;对称轴:直线x=6;顶点坐标:(6,3).216212xxy21描点、连线，画出函数图像.●●●●●●●（6,3）Ox5510216212xxy36212xy问题：1.看图像说说抛物线的增减性。2.怎样平移抛物线可以得到抛物线？216212xxy216212xxy221xy二次函数y=—x－6x+21图象的画法：(1)“化”：化成顶点式；(2)“定”：确定开口方向、对称轴、顶点坐标；(3)“画”：列表、描点、连线。212函数y=ax²+bx+c的顶点是cbxaxy2ccxabxa2提取二次项系数acababxabxa22222配方:加上再减去一次项系数一半的平方222442abacabxa整理:前三项完全平方式,后两项合并同类项.44222abacabxa化简:去掉中括号这个结果通常称为顶点式.224.24bacbyaxaa公式为：归纳总结：•一般地，可以用配方法将配方成abacabxay44)2(22cbxaxy2﹙1﹚二次函数(a≠0)的图象是一条抛物线；cbxaxy2﹙2﹚对称轴是直线；顶点坐标是()x=ab2abacab44,22方法归纳配方法公式法二次函数y=ax2+bx+c(a≠0)的图象和性质１.顶点坐标与对称轴２.位置与开口方向３.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下在对称轴的左侧,y随着x的增大而减小.在对称轴的右侧,y随着x的增大而增大.在对称轴的左侧,y随着x的增大而增大.在对称轴的右侧,y随着x的增大而减小.根据图形填表：abacab44,22abacab44,22abx2直线abx2直线abacabx44,22最小值为时当abacabx44,22最大值为时当1．写出下列抛物线的开口方向、对称轴及顶点坐标．xxy232xxy228822xxy34212xxy（4）（3）（2）（1）练习解:(1)a=3>0抛物线开口向上21233x顶221433y顶11,33顶点坐标为13x对称轴解:a=－1<0抛物线开口向下2121x顶22141y顶1,1顶点坐标为1x对称轴xxy22（2）解:a=－2<0抛物线开口向下8222x顶24288042y顶2,0顶点坐标为2x对称轴8822xxy（3）解:a=0.5>0抛物线开口向上4420.5x顶240.534540.5y顶4,5顶点坐标为4x对称轴34212xxy（4）1.抛物线y=2x2+8x-11的顶点在（）A.第一象限B.第二象限C.第三象限D.第四象限2.不论k取任何实数，抛物线y=a(x+k)2+k(a≠0)的顶点都在（）A.直线y=x上B.直线x=-k上C.x轴上D.y轴上3.若二次函数y=ax2+4x+a-1的最小值是2,则a的值是（）A.4B.-1C.3D.4或-1CBA4.若一次函数y=ax+b的图象经过第二、三、四象限，则二次函数y=ax2+bx-3的大致图象是()xyoxyoxyoxyoABCD-3-3-3-3C例：指出抛...