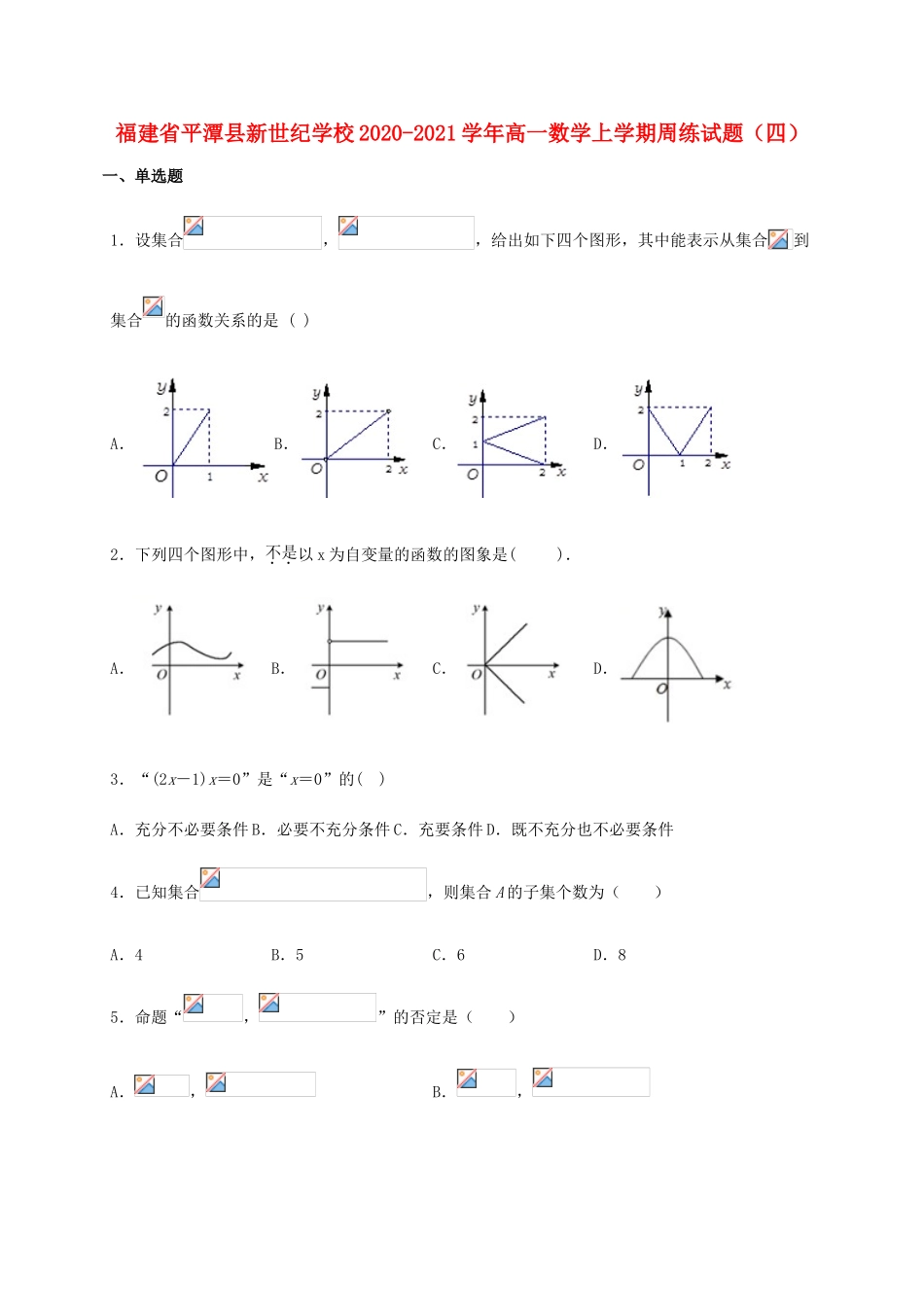
福建省平潭县新世纪学校2020-2021学年高一数学上学期周练试题(四)一、单选题1.设集合,,给出如下四个图形,其中能表示从集合到集合的函数关系的是()A.B.C.D.2.下列四个图形中,不是以x为自变量的函数的图象是().A.B.C.D.3.“(2x-1)x=0”是“x=0”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.已知集合,则集合A的子集个数为()A.4B.5C.6D.85.命题“,”的否定是()A.,B.,C.,D.,6.已知,,,则的最小值为()A.3B.4C.5D.67.若非零实数满足,则下列不等式成立的是()A.B.C.D.8.关于的不等式的解集为()A.B.C.D.二、多选题9.已知集合,集合,下列关系正确的是().A.B.C.D.10.已知关于的不等式的解集为,则()A.B.不等式的解集是C.D.不等式的解集为三、填空题11.若命题“∃x∈R,使得x2+(a-1)x+1<0”是真命题,则实数a的取值范围是______.12.已知集合.若“”是“不等式成立”的充分条件,则实数a的最大值为______.13.设,则函数的最小值为_____14.已知,,且,则的最小值为______.四、解答题15.已知全集,集合,,.(1)求;(2)若,求实数的取值范围.16.一家货物公司计划租地建造仓库储存货物,经过市场调查了解到下列信息:每月土地占地费(单位:万元)与仓库到车站的距离(单位:)成反比,每月库存货物费(单位:万元)与成正比;若在距离车站处建仓库,则和分别为10万元和1.6万元.这家公司应该把仓库建在距离车站多少千米处,才能使两项费用之和最小?并求出这个最小值.17.已知函数.(1)若关于的不等式的解集为,求的值;(2)当时,解关于的不等式.参考答案1.D2.C3.B4.A5.C6.B7.C8.A9.ACD10.ABD11.12.3;13.814.415.(1)或,(2)16.处,最小值为8万元..17.(1);(2)当时,不等式的解集为;当时,不等式的解集为.【详解】(1)由条件知,关于的方程的两个根为1和2,所以,解得.(2)当时,,即,当时,解得或;当时,解得;当时,解得或.综上可知,当时,不等式的解集为;当时,不等式的解集为.