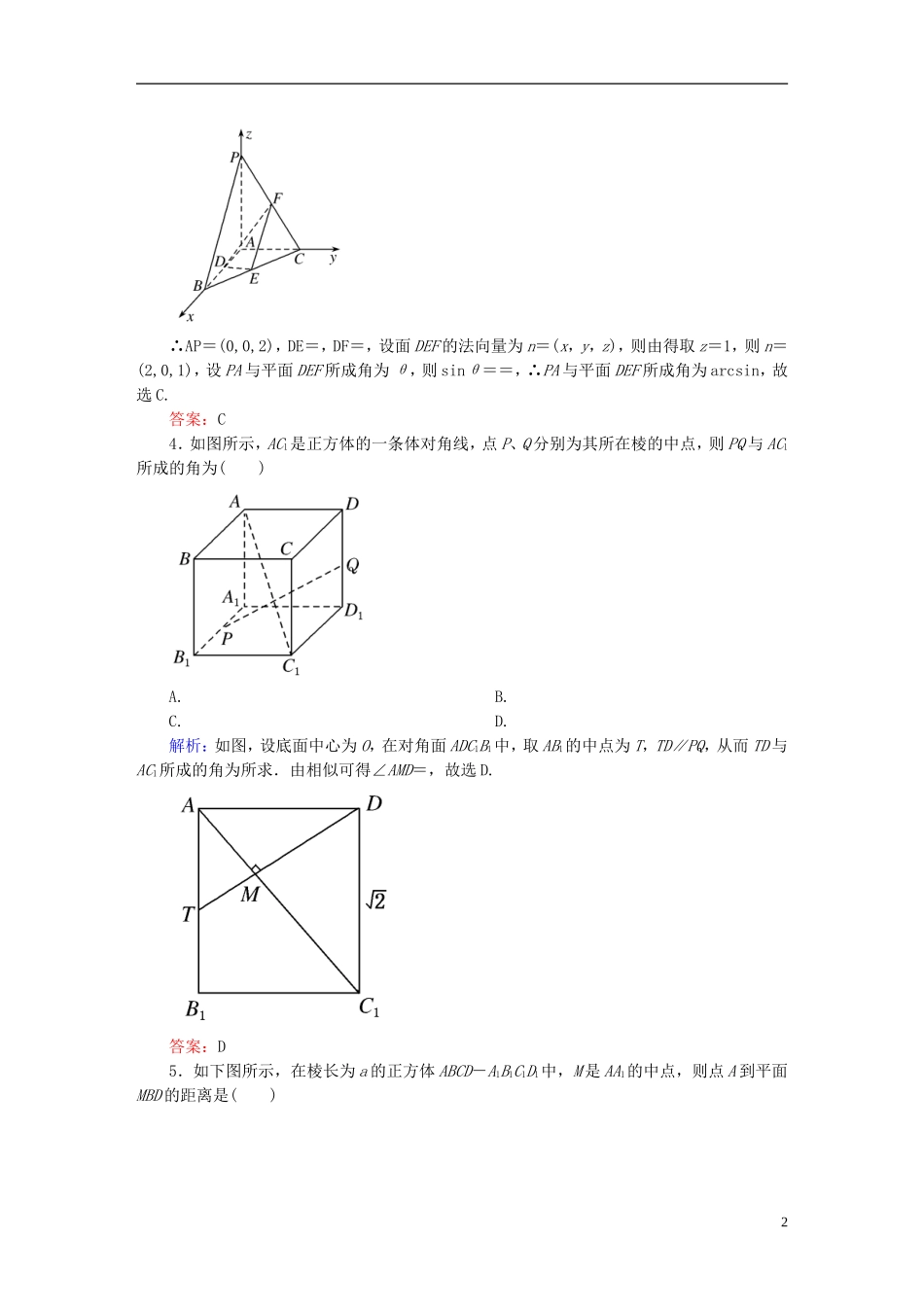
高考专题训练七空间向量与立体几何班级_______姓名________时间:45分钟分值:75分总得分________一、选择题:本大题共6小题,每小题5分,共30分.在每小题给出的四个选项中,选出符合题目要求的一项填在答题卡上.1.在正方体ABCD-A1B1C1D1中,M、N分别为棱AA1和BB1的中点,则sin〈CM,D1N〉的值为()A.B.C.D.解析:以D为原点,DA、DC、DD1分别为x轴、y轴、z轴建系,设正方体棱长为1,则C(0,1,0),M,D1(0,0,1),N,∴CM=,D1N=,∴cos〈CM,D1N〉==-,∴sin〈CM,D1N〉=.故选B.答案:B2.(2011·全国)已知直二面角α-l-β,点A∈α,AC⊥l,C为垂足,B∈β,BD⊥l,D为垂足,若AB=2,AC=BD=1,则D到平面ABC的距离等于()A.B.C.D.1解析:由AB2=(AC+CD+DB)2=AC2+CD2+DB2+2AC·CD+2AC·DB+2CD·DB=1+|CD|2+1,所以|CD|=.过D作DE⊥BC于E,则DE⊥面ABC,DE即为D到平面ABC的距离.在Rt△BCD中,BC2=BD2+CD2=3,∴BC=.DE·BC=BD·CD,∴DE=.答案:C3.在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,D、E、F分别是棱AB、BC、CP的中点,AB=AC=1,PA=2,则直线PA与平面DEF所成角的正弦值为()A.B.C.D.解析:以A为原点,AB、AC、AP所在直线分别为x轴、y轴、z轴建立如图所示空间直角坐标系,由AB=AC=1,PA=2,得A(0,0,0),B(1,0,0),C(0,1,0),P(0,0,2),D,E,F,1∴AP=(0,0,2),DE=,DF=,设面DEF的法向量为n=(x,y,z),则由得取z=1,则n=(2,0,1),设PA与平面DEF所成角为θ,则sinθ==,∴PA与平面DEF所成角为arcsin,故选C.答案:C4.如图所示,AC1是正方体的一条体对角线,点P、Q分别为其所在棱的中点,则PQ与AC1所成的角为()A.B.C.D.解析:如图,设底面中心为O,在对角面ADC1B1中,取AB1的中点为T,TD∥PQ,从而TD与AC1所成的角为所求.由相似可得∠AMD=,故选D.答案:D5.如下图所示,在棱长为a的正方体ABCD-A1B1C1D1中,M是AA1的中点,则点A到平面MBD的距离是()2A.aB.aC.aD.a解析:A到面MBD的距离由等积变形可得.VA-MBD=VB-AMD.易求d=a.答案:D6.已知平面α与β所成的二面角为80°,P为α,β外一定点,过点P的一条直线与α,β所成的角都是30°,则这样的直线有且仅有()A.1条B.2条C.3条D.4条解析:如右图,过P作α、β的垂线PC、PD,其确定的平面与棱l交于Q,过P的直线与α、β分别交于A、B两点,若二面角为80°,AB与平面α、β成30°,则∠CPD=100°,AB与PD、PC成60°,因此问题转化为过P点与直线PD、PC所成角为60°的直线有几条. <60°,<60°,∴这样的直线有4条.答案:D二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡上.7.(2011·全国)已知点E、F分别在正方体ABCD-A1B1C1D1的棱BB1、CC1上,且B1E=2EB,CF=2FC1,则面AEF与面ABC所成的二面角的正切值等于________.解析:如图,以DA,DC,DD1为x轴、y轴、z轴建立空间直角坐标系设正方体的边长为3.3∴A(3,0,0),E(3,3,1),F(0,3,2)∴AE=(0,3,1),AF=(-3,3,2)设平面AEF的法向量为n=(x,y,z),∴⇒令y=1,∴z=-3,x=-1,∴n=(-1,1,-3)又DD1=(0,0,3)为面ABC的一个法向量,设平面AEF与平面ABC所成的二面角为θ∴cosθ=|cos〈n,DD1〉|==∴sinθ==∴tanθ==.答案:8.已知l1,l2是两条异面直线,α、β、γ是三个互相平行的平面,l1、l2分别交α、β、γ于A、B、C和D、E、F,AB=4,BC=12,DF=10,又l1与α成30°角,则β与γ间的距离是________;DE=________.解析:由直线与平面所成角的定义及平行平面距离定义易得β与γ间距离为6.由面面平行的性质定理可得=,∴=,即=.∴DE=2.5.答案:62.59.坐标平面上有点A(-2,3)和B(4,-1),将坐标平面沿y轴折成二面角A-Oy-B,使A,B两点的距离为2,则二面角等于________.解析:如图,AD⊥BC,BC⊥CD,∴BC⊥平面ACD,∴BC⊥AC,AB=2,BC=4,∴AC=2,AD=2,CD=4,∴cosθ==-=-.答案:120°10.已知正方体ABCD-A1B1C1D1的棱长为1,则直线DA1与AC间的距离为________.4解析:设n=λAB+μAD+AA1是A1D和AC的公垂线段上的向量,则n·A1D=(λAB+μAD+AA1)·(...