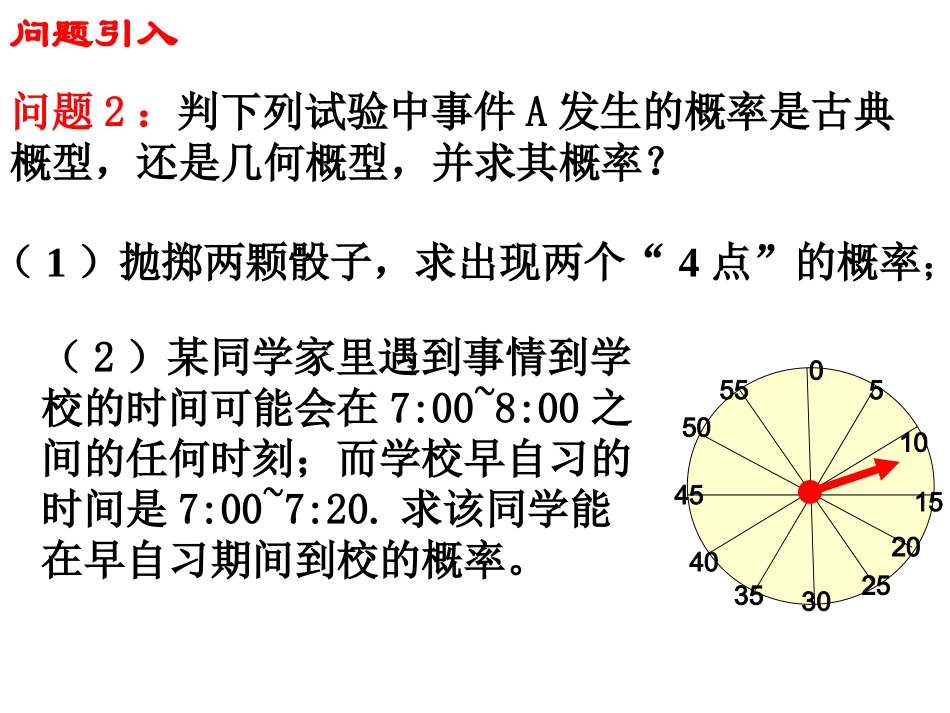
第三章概率复习课必修3问题引入问题1:甲、乙两人下棋,两人下成和棋的概率是0.5,乙获胜的概率是0.2,则乙不输的概率是____,甲获胜的概率是_____,甲不输的概率是____。若把甲获胜记为事件A,乙获胜记为事件B,甲乙和棋记为事件C。上述的一些事件有什么关系呢?问题引入问题2:判下列试验中事件A发生的概率是古典概型,还是几何概型,并求其概率?5520030505101525354045(2)某同学家里遇到事情到学校的时间可能会在7:00~8:00之间的任何时刻;而学校早自习的时间是7:00~7:20.求该同学能在早自习期间到校的概率。(1)抛掷两颗骰子,求出现两个“4点”的概率;例1:黄种人群中各种血型的人所占的比如表所示:血型ABABO该血型的人所占比%2829835已知同种血型的人可以相互输血,O型血可以输给任何一种血型的人,任何人的血都可以输给AB型血的人,其他不同血型的人不能互相输血,小明是B血型,若小明因病需要输血。(1)任找一人,其血可以输给小明的概率是多少;(2)任找一人,其血不能输给小明的概率。例2:一个盒子中有大小相同的3个红球,2个白球,现从中随机取出2个球,求:(1)共有多少个基本事件;(2)两个都是红球的概率;(3)两个颜色不同的概率;(4)至少有一个白球的概率。变式:两人约定于8点到9点有某地会面,试求一人要等另一人半小时之内会面的概率?例3:在区间(0,1)中随机地取出两个数,求两数之和小于6/5的概率。(1)抛掷2颗质地均匀的骰子,求点数和为8的概率。练习:(2)下图是边长为1的正三角形及其内切圆,随机向正三角形内丢一粒芝麻,求芝麻落入圆内的概率为_____________利用古典概型的计算公式时应注意两点:(1)所有的基本事件必须是互斥的;(2)m为事件A所包含的基本事件数,求m值时,要做到不重不漏。小结:古典概型的概率公式事件A所包含的基本事件的个数基本事件的总数P(A)=古典概型一次试验中所有可能出现的基本事件只有有限个(有限性),且每个基本事件出现的可能性相等(等可能性).几何概型每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例.几何概型的概率公式构成事件A的区域长度(面积或体积)试验的全部结果所构成的区域长度(面积或体积)P(A)=概率的几个基本性质(1)0≤P(A)≤1.(2)若事件A与B互斥,则P(A∪B)=P(A)+P(B).(3)若事件A与B对立,则P(A)+P(B)=1.