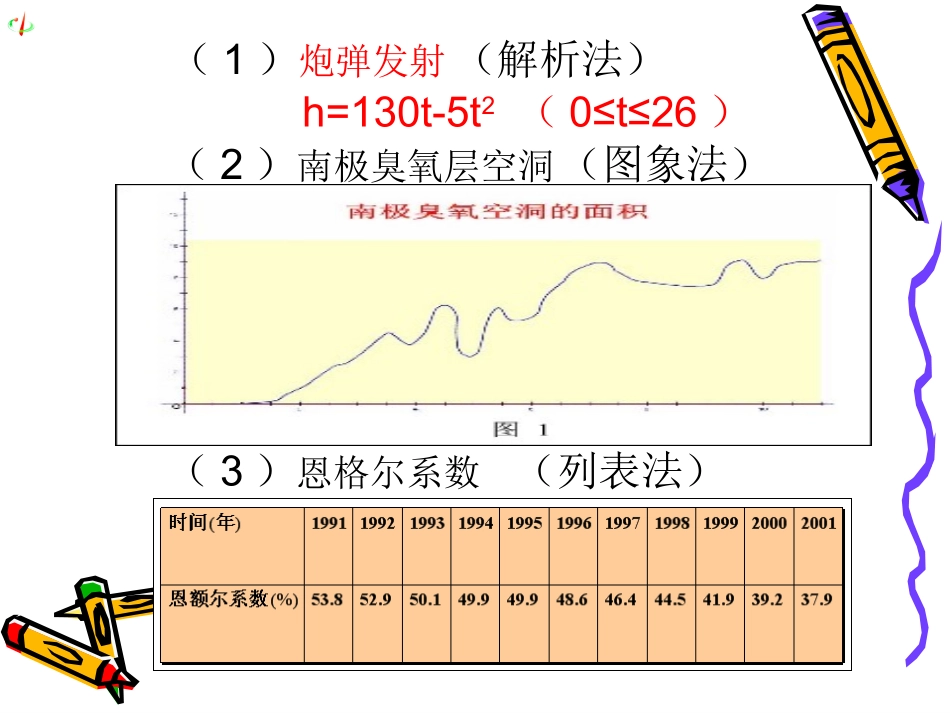
(1)炮弹发射(解析法)h=130t-5t2(0≤t≤26)(2)南极臭氧层空洞(图象法)(3)恩格尔系数(列表法)把两个变量的关系,用一个等式表示,这个等式就叫做函数的解析式.)0(,2,,60:222acbxaxyrlSrAtS如优点:函数关系清楚,给定自变量能直接算出函数值,便于研究函数性质.1.解析法:函数的表示法2.列表法:优点:不用计算便可知道自变量对应的函数值。列出表格来表示两个变量的关系.如:平方表,平方根表,汽车、火车站的里程价目表、银行里的“利率表”等等.优点:直观形象,便于了解函数的性质.yOx3.图象法:如:一次函数的图象是一条直线;如函数y=kx+b(k<0、b>0)用函数图象来表示两个变量之间的关系.下列图形中可化为函数y=f(x)图像的是()xy0(A)xy0(B)xy0(C)xy0(D)D任作垂直于x轴的直线,若此直线与图像只有一个交点,则图像能表示函数的图像,即要保证一个x值对应唯一的一个y值.小结:判断一个图像是不是函数的法则:例1.某种笔记本每个5元,买x(x∈{1,2,3,4})个笔记本的钱数记为y(元),试写出以x为自变量的函数y的解析式,并画出这个函数的图象.解:这个函数的定义域是数集{1,2,3,4,5}用解析法可将函数y=f(x)表示为用列表法可将函数表示为5,4,3,2,1,5xxy笔记本数x钱数y1122334455551010151520202525用图象法可将函数表示为下图....12345x0510152025y.用描点法画函数图象的一般步骤是什么?列表、描点、连线(视其定义域决定是否连线)笔记本数笔记本数xx1122334455钱数钱数yy551010151520202525函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等等.例2.画出函数y=|x|的图象.图象如下:解:00xxyxx-2-30123xy12345-1..分段函数是一个函数,不要误以为是几个函数有些函数在它的定义域中,对于自变量的不同取值范围,对应关系不同,这种函数通常称为分段函数。【例2】下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表。第一第一次次第二次第二次第三次第三次第三次第三次第五次第五次第六次第六次王伟王伟989887879191929288889595张城张城909076768888757586868080赵磊赵磊686865657373727275758282班级平均分班级平均分88.288.278.378.385.485.480.380.375.775.782.682.6表格能否直观地分析出三位同学成绩高低?如何才能更好的比较三个人的成绩高低?解:将“成绩”与“测试时间”之间的关系用函数图象表示出来。可以看出:王伟同学学习情况稳定且成绩优秀;张城同学的成绩在班级平均水平上下波动,且波动幅度较大;赵磊同学的成绩低于班级平均水平,但成绩在稳步提高。分段函数的表达式虽然不止一个,但它不是几个函数,而是一个函数.函数在它的定义域中,对于自变量x的不同取值范围,对应关系不同,这种函数通常称为分段函数.分段函数的定义一般地,设A、B是两个集合,如果按照某种对应法则f,对于集合A中的任一个元素,在集合B中都有唯一的元素和它对应,那么这样的对应(包括A、B以及A到B的对应法则f)叫做集合A到集合B的一个映射.映射的定义:函数的定义设A、B是非空数集,如果按照某种对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),xA∈一种对应是映射,必须满足两个条件:①A中任何一个元素在B中都有元素与之对应(至于B中元素是否在A中有元素对应不必考虑,即B中可有“多余”元素).②B中所对应的元素是唯一的(即“一对多”不是映射,而“多对一”可构成映射).理解:例1.判断下列对应是否映射?有没有对应法则?abcefgabcdefg是不是是1、3是映射,有对应法则,对应法则是用图形表示出来的.abcefgd象与原象的定义:③求正弦906045301232221④乘以2123123456给定一个集合A到B的映射,且a∈A,b∈B,若a与b对应,则把元素b叫做a在B中的象,而a叫做b的原象.注意:(1)集合A到B的映射中,A、B必须是非空集合;(2)对应关系f具有“方向性”,即从集合A到B的映射,与从集合B到A的映射一般是不同的;(3)对于映射f:A→B,必须具备以下几点:①A中的每个元素在B中必有唯一的元素与之对...