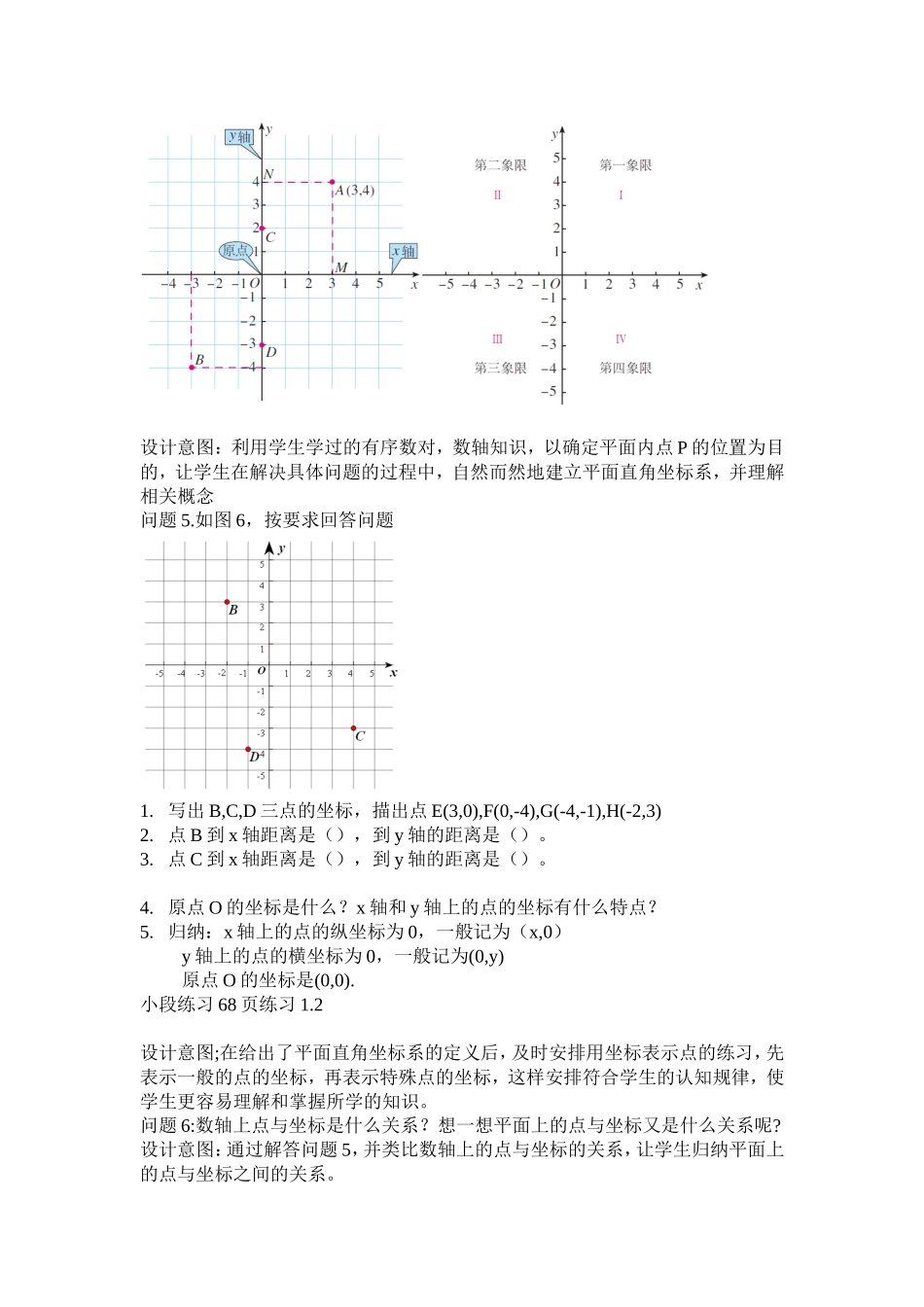
7.1.2平面直角坐标系(第一课时)教学目标:1.知识与技能:理解平面直角坐标系的相关概念,掌握平面直角坐标系内点与坐标是一一对应的关系.2.过程与方法:类比数轴上点的坐标抽象出平面直角坐标系中点与坐标的一一对应关系.3.情感态度与价值观:在探究活动中,体验数学活动中的探索性和创造性,培养严谨的科学态度和较强的抽象思维能力.重点:平面直角坐标系及相关概念.难点:理解建立平面直角坐标系的必要性,体会平面直角坐标系中点与坐标的一一对应的关系.教学过程设计一复习引入问题1:回顾已学内容,回答下列问题:1.什么是数轴?请画出一条数轴.2.如图1,A,B两点所表示的数分别是什么?在数轴上描出“-3”表示的点。问题2:在数轴上已知点能说出它的坐标,由坐标能在数轴上找到对应点的位置,那么数轴上的点与坐标有怎样的关系呢?设计意图;问题1,2从学生的熟悉的数轴出发,给出数轴上点的坐标的定义,建立点与坐标的一一对应的关系。二.探究新知问题3.类似于利用数轴确定直线上点的位置,结合上节课学习的有序数对,回答问题,如图,你能找到一种办法确定平面内点P的位置吗?问题4.如图,学生看书第66,67页后回答下列问题。1.说一说组成平面直角坐标系的两条数轴具备什么特征?2.什么是横轴,什么是纵轴,什么是原点?3.坐标平面被两条坐标轴分成了哪几个部分,分别对应什么象限?设计意图:利用学生学过的有序数对,数轴知识,以确定平面内点P的位置为目的,让学生在解决具体问题的过程中,自然而然地建立平面直角坐标系,并理解相关概念问题5.如图6,按要求回答问题1.写出B,C,D三点的坐标,描出点E(3,0),F(0,-4),G(-4,-1),H(-2,3)2.点B到x轴距离是(),到y轴的距离是()。3.点C到x轴距离是(),到y轴的距离是()。4.原点O的坐标是什么?x轴和y轴上的点的坐标有什么特点?5.归纳:x轴上的点的纵坐标为0,一般记为(x,0)y轴上的点的横坐标为0,一般记为(0,y)原点O的坐标是(0,0).小段练习68页练习1.2设计意图;在给出了平面直角坐标系的定义后,及时安排用坐标表示点的练习,先表示一般的点的坐标,再表示特殊点的坐标,这样安排符合学生的认知规律,使学生更容易理解和掌握所学的知识。问题6:数轴上点与坐标是什么关系?想一想平面上的点与坐标又是什么关系呢?设计意图:通过解答问题5,并类比数轴上的点与坐标的关系,让学生归纳平面上的点与坐标之间的关系。活动三练习一:基础巩固(全体学生)1.在平面直角坐标系中,点P(2,-3)在()A.第一象限B.第二象限C第三象限D第四象限2.若第二象限内的点P(x,m),满足︱X︱=3,㎡=25,则点P的坐标是_3.已知点P(3,a-1)到两坐标轴的距离相等,则a的值是_A.4B.3C.-2D.4或-24.点P(m+3,m-1)在X轴上,则点P的坐标为_A.(0,-2)B.(2,0)C.(4,0)D.(0,-4)5.点P(x,x-2)一定不在第_象限。师生行为:教师提出问题,学生独立完成后组内交流。教师关注:1.学生能否熟练地运用平面直角坐标系的相关知识点解决问题。2.学生能否积极参与合作交流。设计意图:通过这5道题,进一步让学生体会各象限内点的符号特点,坐标轴上点的坐标特点,距离在实际问题中应用,让学生在独立思考的基础上,参与对问题的讨论,锻炼学生的表达能力,培养学生的合作意识。练习二:能力提升(A,B组学生完成)设M(a,b)为平面直角坐标系中的点,1)当a>0,b<0时,点M位于第几象限?2)当ab>0时,点M位于第几象限?3)当a为任意实数,且b<0时,点M位于何处?师生行为:教师提出问题,学生先独立思考,自主解决,然后交流,并展示。教师关注:1.学生能否认真独立思考。2.学生能否积极参与合作交流。3.学生能否把所学知识联系在一起。4.学生能否清楚地表达自己的解题思维。设计意图:通过这一道题让学生学会用各象限内的点的符号特点解决问题,让学生在独立思考的基础上,参与对问题的讨论,锻炼学生的表达能力,,培养学生的合作意识。练习三:拓广探索(A组学生完成)已知点O(0,0),B(1,2),点A在坐标轴上,且S△OAB=2,求满足条件的点A的坐标。师生行为:教师出示问题,学生先独立思考,自主解决,然后交流,并展示。教师关注:1.学生能否把所学知识与实际问题联系在一起。2.学生...