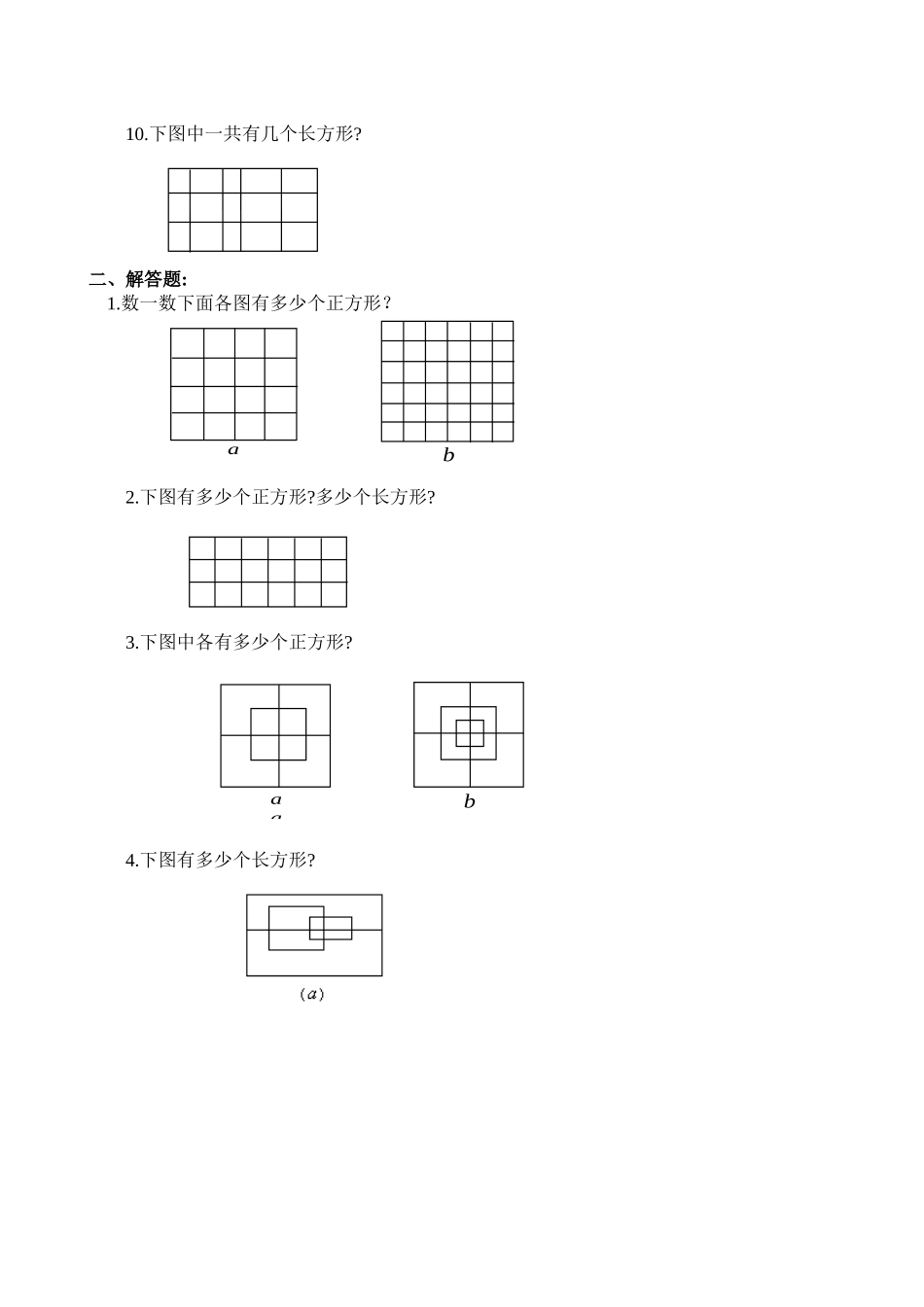
十、数线段与长方形(A)年级______班_____姓名_____得分_____一、填空题:1.下列图形各有几条线段()条()条()条2.在一线段上任取21个点,(包括两端点).则一共有()条线段.3.下图一共有()条线段:4上中图形中,一共有()个角.5.数一数,右图中一共有()个角.6.一条直线上共有50个点,可以数出()条线段.7.从一点引出10条射线,可以数出()个小于1800的角.8.平面上有10个点,设有三点在一直线上的情况.这些点可以连成()条线段.9.把一个三角形底边平均分成20等份,等分点与顶点相连,可以连成()条线段.10.右图中,大大小小的长方形一共有()个.二、解答题:1.下图中,一共有几个长方形?2.右上图中一共有几个长方形?3.右图中大大小小的长方形共有多少个?4.右图中共有多少个长方形?十、数线段与长方形(B)年级______班_____姓名_____得分_____一、填空题:1.数一数下图共有()条线段.()条.()条.2.数一数下图共有()条线段.()条.()条.3.下列图中各有几个三角形:4.下图中各有()个三角形.5.下图中有()个长方形.6.数一数下图有()个长方形.7.下图共有()个长方形.8.数一数图中长方形的个数.9.数一数下面各图有多少个长方形.BDCA③DCABDCBABADC(a)(b)10.下图中一共有几个长方形?二、解答题:1.数一数下面各图有多少个正方形?2.下图有多少个正方形?多少个长方形?3.下图中各有多少个正方形?4.下图有多少个长方形?abaab———————————————答案——————————————————————分析与解答一、填空题:1.a有10条,b有15条,c有21条.2.(1+2+3+4+……+19+20)点金术:如果线段上的基本线段有n条,则=(20+1)¿20¿2总的线段数为:=210(条).1+2+3+4+……+(n−1)+n=(1+n)×n÷¿¿23.(1+2)¿4+(3+2+1)¿2点金术:如果图形比较复杂时,可以先找出=12+12线段条数相等的线段,再加起来.=24(条).4.6+5+4+3+2+1点金术:如果一个角内一共有几个基本角.=21(个).则总的角(锐角)一共有(n+1)×n÷¿¿2.5.(1+99)¿99¿2=99¿50=4950(个).6.50¿49¿2=1225(条).7.10¿9¿2=45(个).8.10¿9¿2=45(条).9.(1+20)¿20¿2+19=229(个).10.(5+4+3+2+1)¿1=15(个).二、解答题:1.一共有(5+4+3+2+1)¿(2+1)=45(个).2.解:一共有90(个).(5+4+3+2+1)¿(3+2+1)=(6¿5¿2)¿(4¿3¿2)=15¿6=90(个).注:一般地有如下规律:长方形个数=[(长边段数+1)¿长边段数¿2]¿[(宽边段数+1)¿宽边段数¿2]3.共有102个.解:①长方形ABDE内包含的长方形的个数有:(6¿5¿2)¿(4¿3¿2)=90(个).②长方形CDFG内包含的长方形个数有:(3¿2¿2)¿(5¿4¿2)=30(个).③在上面的两项计算中,长方形CDEH内的长方形被重复计算了,这部分长方形的个数是:(3¿2¿2)¿(4¿3¿2)=18(个).④图中共有长方形:90+30-18=102(个).4.解:①左边大长方形内有长方形:(5+4+3+2+1)¿(7+6+5+4+3+2+1)=15¿28=420(个).②下边大长方形内有长方形:(4+3+2+1)¿(8+7+6+5+4+3+2+1)=10¿36=360(个).③左下重复的长方形有:(4+3+2+1)¿(7+6+5+4+3+2+1)=10¿28=280(个).④图中共有长方形:420+360-280=500(个).———————————————答案——————————————————————一、填空题:1.16;30.2.36;27.3.①18;②27;③20.4.①33;②24.5.10个.图中长方形的个数与AB边上所分成的线段的条数有关,每一条线段对应一个长方形,所以长方形的个数等于AB边上线段的条数,即长方形个数为:4+3+2+1=10(个).6.30个.图中AB边上共有线段4+3+2+1=10条.BC边上共有线段:2+1=3(条),把AB上的每一条线段作为长,BC边上每一条线段作为宽,每一个长配一个宽,就组成一个长方形,所以图中共有长方形为:(4+3+2+1)¿(2+1)=10¿3=30(个).7.60个.图中,依据计算上图中长方形个数的方法:可得长方形个数为:(4+3+2+1)¿(3+2+1)=60(个).一般情况下,如果有类似图中的任一个长方形一边上有n−1个分点(不包括这条边的两个端点),另一边上有m−1个分点(不包括这条边的两个端点),通过这些点分别作对边的平行线且与另一边相交,这两组平行线将长方形分为许多长方形,这时长方形的总数为:(1+2+3+……+m)¿(1+2+3+……n).8.共有90个.AB边上分成的线段有:5+4+3+2+1=15.BC边上分成的线段有:3+2+1=6.所以共有长方形:(5+4+3+2+1)¿(3+2+1)=15¿6=90(个).9.15个;45个.10.(3+2+1)¿(5+4+3+2+1)=6¿15=90(个).二、解答题:1.a:4¿4+3¿3+2¿2+1¿1=30(个)b:6¿6+5¿5+4¿4+3¿3+2¿2+1=91(个)2.32个正方形.126个长方形.3.a:10个.b:15个.4.15个.