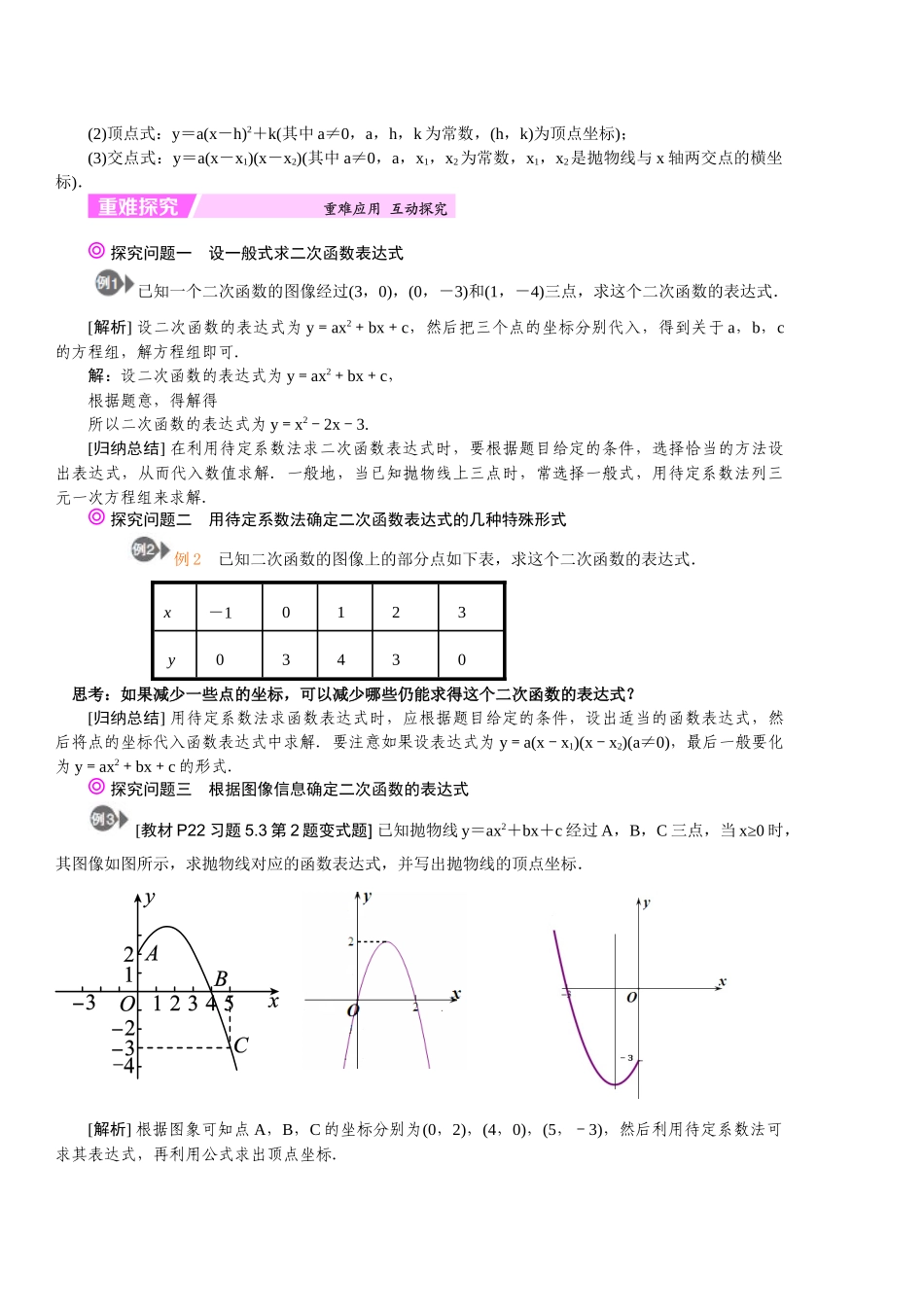
5.3用待定系数法确定二次函数表达式本课教材分析:教材的地位和作用二次函数是初中数学的重要内容之一,而用待定系数法求函数表达式在前面的一次函数,反比例函数中已经多次得以运用,确定一次函数有两个独立系数,要两个独立条件,这些知识方法同学们已熟悉,本节把这些所学知识推向初中学段的最高点——二次函数表达式的确定.由于前几节已经对二次函数的表达式进行了多方面的认识,是学习本节最直接的认知基础,通过本节的学习,进一步深化对二次函数的认识教学目标知识与技能通过对用待定系数法求二次函数表达式的探究,掌握求函数表达式的方法过程与方法灵活地根据条件恰当地选择表达式,体会二次函数表达式之间的转化情感、态度与价值观从学习中体会数学知识的价值,从而提高学生学习数学知识的兴趣教学重点难点重点用待定系数法求函数表达式难点根据不同的条件灵活地选择恰当的表达式,从而用待定系数法求函数表达式易错点不能根据条件正确地设函数表达式或解方程组而出错教学过程活动1知识准备1.若反比例函数经过点(-2,3),则反比例函数的表达式为__y=-__.2.若一次函数经过点(2,0),(0,2),则一次函数的表达式为__y=-x+2__.活动2教材导学学会用待定系数法求二次函数表达式阅读教材P21,完成下列各题:1.已知二次函数y=ax2-2的图像经过点(1,-1),则这个二次函数的表达式为__y=x2-2__.2.已知二次函数y=x2+bx+c的图像经过点(1,0)和(0,1),则这个二次函数的表达式为__y=x2-2x+1__.◆知识链接——[新知梳理]知识点一►知识点一用待定系数法求二次函数表达式的一般步骤(1)设二次函数的表达式;(2)列方程组求待定系数;(3)解待定系数;(4)还原.►知识点二二次函数表达式有三种形式(1)一般式:y=ax2+bx+c(其中a≠0,a,b,c为常数);(2)顶点式:y=a(x-h)2+k(其中a≠0,a,h,k为常数,(h,k)为顶点坐标);(3)交点式:y=a(x-x1)(x-x2)(其中a≠0,a,x1,x2为常数,x1,x2是抛物线与x轴两交点的横坐标).探究问题一设一般式求二次函数表达式已知一个二次函数的图像经过(3,0),(0,-3)和(1,-4)三点,求这个二次函数的表达式.[解析]设二次函数的表达式为y=ax2+bx+c,然后把三个点的坐标分别代入,得到关于a,b,c的方程组,解方程组即可.解:设二次函数的表达式为y=ax2+bx+c,根据题意,得解得所以二次函数的表达式为y=x2-2x-3.[归纳总结]在利用待定系数法求二次函数表达式时,要根据题目给定的条件,选择恰当的方法设出表达式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解.探究问题二用待定系数法确定二次函数表达式的几种特殊形式例2已知二次函数的图像上的部分点如下表,求这个二次函数的表达式.x-10123y03430思考:如果减少一些点的坐标,可以减少哪些仍能求得这个二次函数的表达式?[归纳总结]用待定系数法求函数表达式时,应根据题目给定的条件,设出适当的函数表达式,然后将点的坐标代入函数表达式中求解.要注意如果设表达式为y=a(x-x1)(x-x2)(a≠0),最后一般要化为y=ax2+bx+c的形式.探究问题三根据图像信息确定二次函数的表达式[教材P22习题5.3第2题变式题]已知抛物线y=ax2+bx+c经过A,B,C三点,当x≥0时,其图像如图所示,求抛物线对应的函数表达式,并写出抛物线的顶点坐标.[解析]根据图象可知点A,B,C的坐标分别为(0,2),(4,0),(5,-3),然后利用待定系数法可求其表达式,再利用公式求出顶点坐标.解:由图像可知A(0,2),B(4,0),C(5,-3),∴解得∴抛物线的表达式为y=-x2+x+2.∴-=-=,==,∴其顶点坐标为.[归纳总结]利用图像信息求函数表达式的关键是找出图像上有关点的坐标,然后将点的坐标代入表达式中,列出关于未知系数的方程组,然后求出各未知系数即可.[课堂小结][反思]已知二次函数图像的对称轴是直线x=-1,与y轴交点的纵坐标是-6,且经过点(2,10),求此二次函数的表达式.[答案]y=2x2+4x-6.课后作业:一、填空题1.如果二次函数y=(a-1)x2-2x+a2+2a-3的图像经过原点,那么a的值为()A.0B.-1...