9.1.1不等式的性质(1)VIP免费

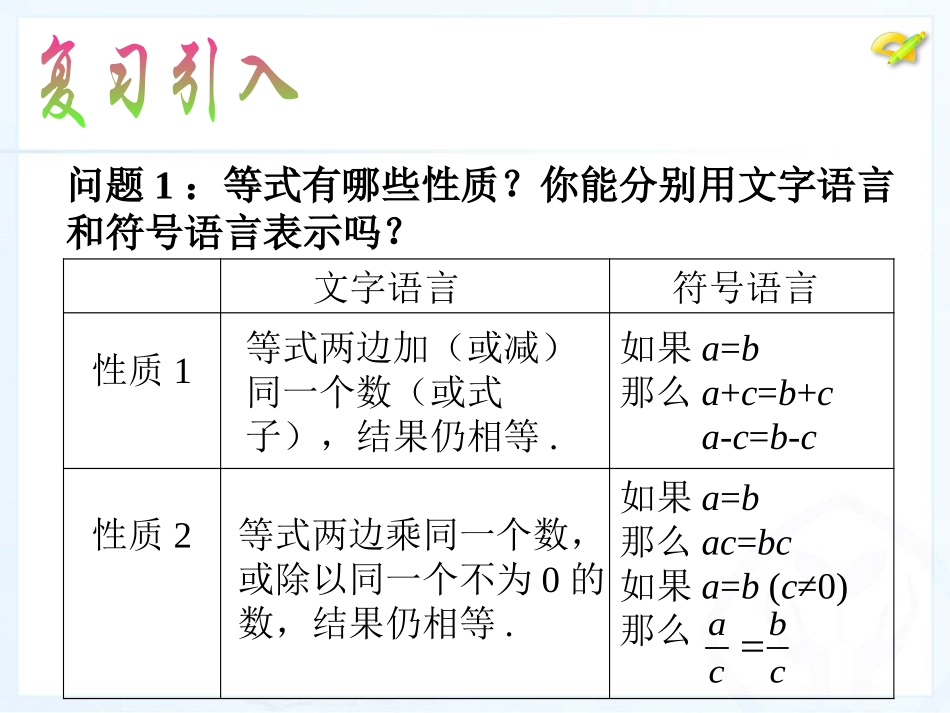
9.1.2不等式的性质（第1课时）学习目标：（1）探索并理解不等式的性质.（2）体会探索过程中所应用的归纳和类比的数学思想方法．学习重点：探索不等式的性质．学习难点：正确应用不等式的三条性质进行不等式的变形9.1.2不等式的性质问题1：等式有哪些性质？你能分别用文字语言和符号语言表示吗？abcc性质1性质2文字语言符号语言等式两边加（或减）同一个数（或式子），结果仍相等.如果a=b那么a+c=b+ca-c=b-c等式两边乘同一个数，或除以同一个不为0的数，结果仍相等.如果a=b那么ac=bc如果a=b(c≠0)那么不等式两边都加上（或减去）同一个数不等号方向是否改变了5＞35＋23＋25＞35－23－2－1＜3－1＋23＋2－1＜3－1－33－3－4＞－6－4＋c－6＋c－4＞－6－4－c－6－c………没有改变没有改变你发现了什么规律？＞＜没有改变没有改变＞＜没有改变没有改变＞＞不等式的两边都加上（或减去）同一个数(或式子)，不等号的方向不变。不等式的性质1：用式子表示：如果a＞b,那么a＋c＞b＋c(或a－c＞b－c)如果a＜b,那么a＋c＜b＋c(或a－c＜b－c)不等式两边都乘以（或除以）同一个正数不等号方向是否改变了6＞26×52×56＞26÷22÷2－2＜3(－2)×63×6－2＜3(－2)÷63÷6－4＞－6－4×2－6×2－4＞－6－4÷2－6÷2………没有改变没有改变＞＜没有改变没有改变＞＜＞＞没有改变没有改变你发现了什么规律？不等式的两边都乘（或除）同一个正数，不等号的方向不变。不等式的性质2：用式子表示：如果a＜b,且c＞0,那么ac＜bc;a÷c＜b÷c如果a＞b,且c＞0,那么ac＞bc;a÷c＞b÷c如图所示，a和b的大小关系如何，从左到右如何变化？讨论：能不能就此认为“不等式的两边都乘以同一个数，所得到的不等式符号不变。”×3×3不等式两边都乘以（或除以）同一个负数不等号方向是否改变了6＞26×(－5)2×(－5)6＞26÷(－2)2÷(－2)－2＜3(－2)×(－6)3×(－6)－2＜3(－2)÷(－6)3÷(－6)－4＞－6－4×(－2)－6×(－2)－4＞－6－4÷(－2)－6÷(－2)………有改变有改变＞＜有改变有改变＞＜你发现了什么规律？＜＜有改变有改变不等式的性质3：用式子表示：不等式的两边都乘（或除）同一个负数，不等号的方向改变。如果a＜b,且c＜0,那么ac＞bc;a÷c＞b÷c如果a＞b,且c＜0,那么ac＜bc;a÷c＜b÷c1、设m>n,选择恰当的不等号填空，并说出理由。(1)m－5_____n－5(2)m＋4_____n＋4(3)6m_____6n(4)3n_____3m2、设a>b,选择恰当的不等号填空，并说出理由。(1)2a－5_____2b－5(2)－3.5a＋1_____－3.5b＋1＜＞＞＞＞＜⑴若a＞-b,则a+b0;⑵若-a＜b,则a－b;⑶若-a＞-b,则2-a2-b;⑷若a＞0,且(1-b)a＜0,则b1.＞＞＞＞例1：利用不等式的性质解下列不等式：x－7>26言必有“据”x>33033根据不等式的性质1，不等式两边都加7，得：x－7+7>26+7利用不等式的性质解下列不等式:3728)4(34)3(5032)2(123)1(xxxxxx讨讨论论：：讨讨论论：：能说出你这节课的收获和体验，你能与大家分享吗？必做：教科书习题9.1第4、6题．选做：教科书复习题9第5题．yyyx4)7(63)2(52121）（解不等式：ab2ab22ba3505－35－5－5abba2__223430>250>3430>5050=___222的大小关系是与猜想根据上述数学实验，abbaabba2222．探究新知问题6等式性质与不等式性质的主要区别是什么？2．探究新知问题6等式性质与不等式性质的主要区别是什么？2．探究新知问题6等式性质与不等式性质的主要区别是什么？3．运用新知例2设，则下列不等式中，成立的是（）.ba66ba（A）（B）（C）（D）ba3322ba11baC3．运用新知练习设,用“＜”或“＞”填空．mn①②③55mn2525mn3.553.55mn＞＞＜4．归纳总结（1）不等式的性质是什么？不等式性质与等式性质的联系与区别是什么？（2）在研究不等式的性质的基本过程中体现了什么数学思想方法？