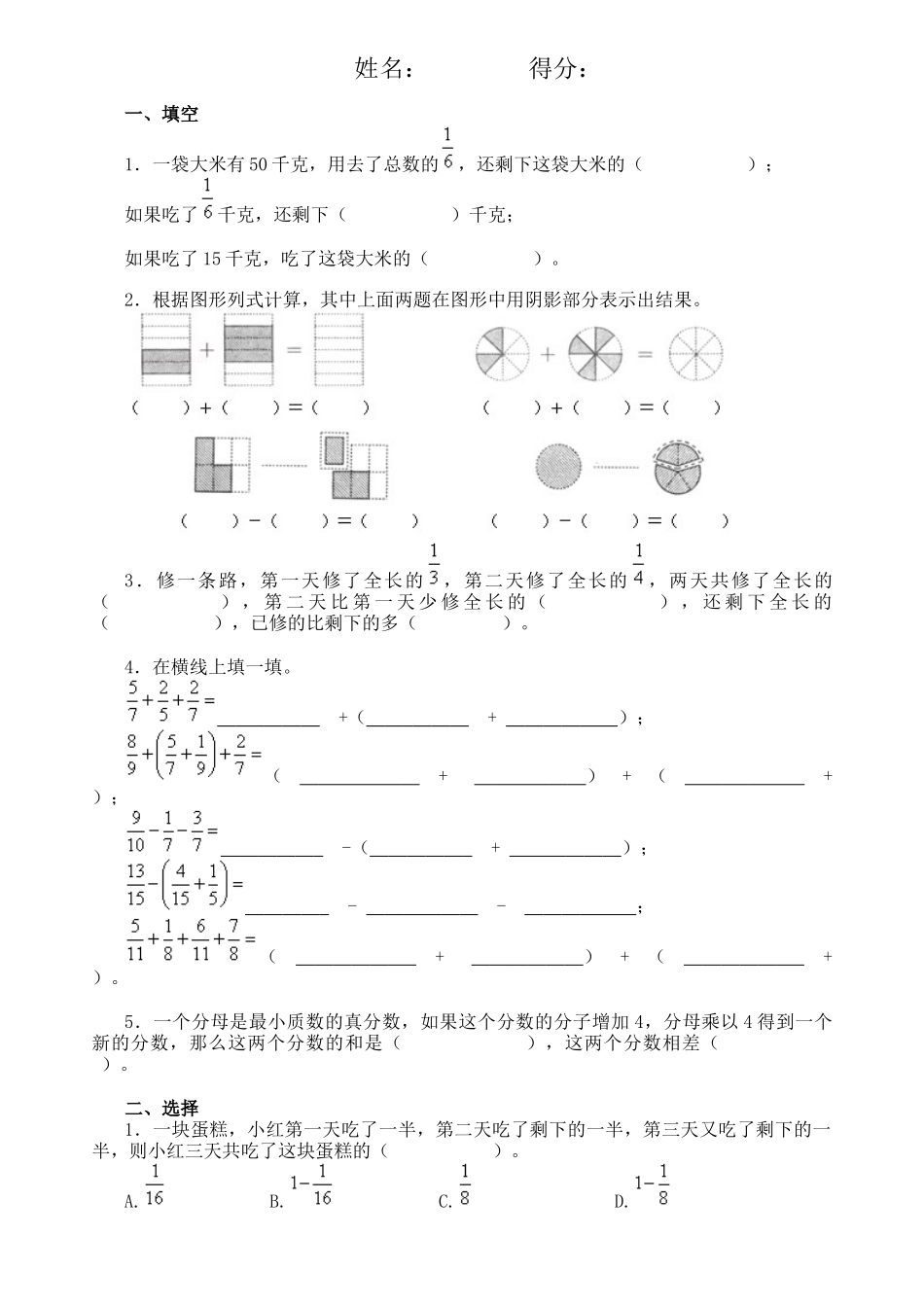
四年级下册乘法运算定律专项练习姓名:_______得分:_______1、乘法交换律:交换两个因数的位置,积不变。用字母表示为:a×b=b×a2、多个数相乘,任意交换因数的位置,积不变。如a×b×c×d=b×d×a×c3、乘法结合律:三个数相乘,先乘前两个数,或者先乘后两个数,积不变。永宁字母表示为:(a×b)×c=a×(b×c)4、在乘法算式中,如果其中两个因数的积为整十、整百、整千数时,可以运用乘法交换律、乘法结合律来改变运算顺序,从而简化运算。如:125×25×8×4=125×8×25×4----------------------------乘法交换律=(125×8)×(25×4)-----------------乘法结合律=1000×100=1000004、乘法交换律、乘法结合律的结合运用(125×12)×8(25×3)×4(25×125)×8×425×125×8×45、运用乘法交换律、乘法结合律简化运算的实质与算式特点实质:把其中相乘结果为整十、整百、整千的两个因数先相乘。通常利用的算式是:2×5=10;4×25=100;8×125=1000;625×16=10000;25×8=200;75×4=300;375×8=3000.特点:连乘‘6、在乘法算式中,当因数中有25、125等因数,而另外的因数没有4或8时,可以考虑将另外的因数分解为两个因数相乘、其中一个因数为4或8的形式,从而利用乘法交换律、乘法结合律使运算简化。4、将因数分解125×3265×16×12548×5×1254、乘法交换律:a×b=b×a25×37×475×39×465×11×45、乘法结合律:(a×b)×c=a×(b×c)38×25×442×125×86×(15×9)25×(4×12)三、乘法分配律1、乘法分配律:两个数的和与一个数相乘,可以先把他们与这个数分别相乘,再把所得的积相加。用字母表示为:(a+b)×c=a×c+b×c2、两个数的差与一个数相乘,可以把它们分别与这个数相乘,再把所得的积相减。用字母表示为:(a-b)×c=a×c-b×c4、以上几个算式均可以逆用,即:a×c+b×c=(a+b)×ca×c-b×c=(a-b)×c5、乘法分配律的理解:以上几个算式应注意利用乘法的意义进行理解:a+b个c等于a个c加上b个c,而不能单纯地依靠记忆,只有这样才能在运算中熟练运用,减少失误。6、乘法分配律的实质与特点:实质:利用乘法的意义将算式转化为整十、整百数的乘法运算。特点:两个积的和或差,其中两个积的因数中有一个因数相同;或两数的和或差乘一个数。7、当算式中没有相同的因数时,考虑利用倍数关系找到相同因数。7、利用倍数关系找到相同因数。246×32+34×49235×28+7021×48+84×1368×57—34×148、当因数与整十、整百数接近时,可以转化为分配律进行简化运算。88×10299×2675×988、乘法分配律(125+9)×864×64+36×6425×6+25×499×99+9989×99+8999×38+389、(a—b)×c=a×c—b×c64×15—14×15102×59—59×2456×25—25×56124×25—25×24101×897—89776×101—76101×26—26101×37—37五年级数学分数加法和减法测试姓名:得分:一、填空1.一袋大米有50千克,用去了总数的,还剩下这袋大米的();如果吃了千克,还剩下()千克;如果吃了15千克,吃了这袋大米的()。2.根据图形列式计算,其中上面两题在图形中用阴影部分表示出结果。3.修一条路,第一天修了全长的,第二天修了全长的,两天共修了全长的(),第二天比第一天少修全长的(),还剩下全长的(),已修的比剩下的多()。4.在横线上填一填。+(+);(+)+(+);-(+);--;(+)+(+)。5.一个分母是最小质数的真分数,如果这个分数的分子增加4,分母乘以4得到一个新的分数,那么这两个分数的和是(),这两个分数相差()。二、选择1.一块蛋糕,小红第一天吃了一半,第二天吃了剩下的一半,第三天又吃了剩下的一半,则小红三天共吃了这块蛋糕的()。A.B.C.D.2.小明做数学作业用了小时,比做语文作业多用小时,他做完这两种作业一共用了多少时间?列式正确的是()。A.B.C.D.3.如下图,已知各种图形的面积都相等,那么可以在“=”后面表示阴影部分面积运算结果的是()。A.B.C.D.4.在中,必须去掉(),才能使余下的分数之和等于1。A.和B.和C.和D.和5.估计一下算式的结果,最接近下列数中的()。A.B.C.1D.2三、解答1.小英生...