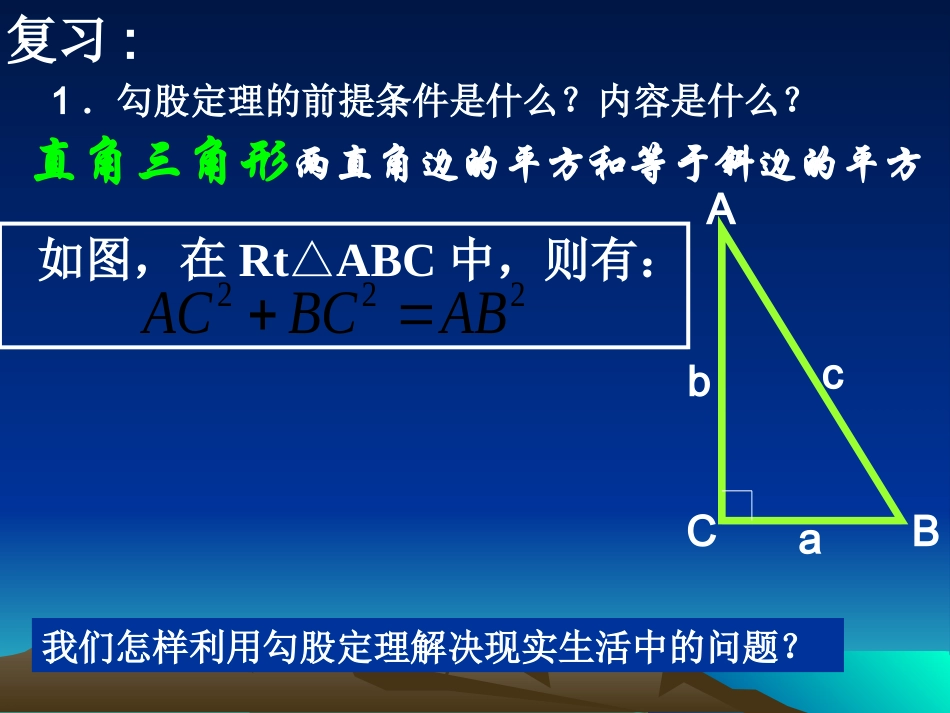
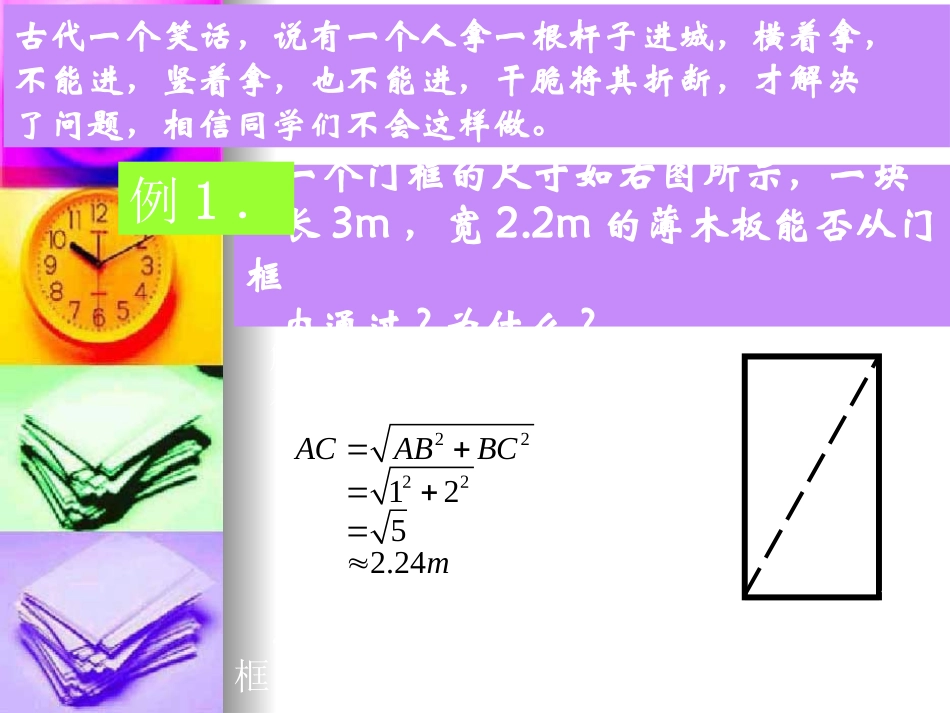
(一)复习:1.勾股定理的前提条件是什么?内容是什么?直角三角形两直角边的平方和等于斜边的平方ABCabc如图,在RtABC△中,则有:222ACBCAB我们怎样利用勾股定理解决现实生活中的问题?古代一个笑话,说有一个人拿一根杆子进城,横着拿,不能进,竖着拿,也不能进,干脆将其折断,才解决了问题,相信同学们不会这样做。ABCD1m2m一个门框的尺寸如右图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?解:连结AC在RtABC△中22221252.24ACABBCm∵AC>2m∴将薄木板的宽斜着放就可以通过此门框例1.练习:如图,从电杆离地面5米处向地面拉一条7米长的钢缆,求地面钢缆固定点A到电杆底部B的距离.(结果保留1位小数)c5米7米解:在Rt△ABC中2222754.9(ABACBC米)答:所求的距离AB约为4.9米【小结】掌握和灵活运用勾股定理例2.如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.(精确到0.01cm)DCB'AA'B222241011610.77()ACABBCcm解:如右图,在Rt△ABC中,BC=底面周长的一半=10cm,答:最短路程约为10.77cm.【小结】①掌握把空间立体几何图形展开成平面图形②在解决空间立体几何图形中的距离问题时,先把几何体适当展开成平面图形,再利用“两点之间线段最短”分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.即AB长为最短路线.(如图)练习:小良家有一底面周长为24m,高为6m的圆柱形罐,一天他发现一只聪明的蟑螂从距底面1m的A处爬行到对角B处,你知道小良为什么说那是只聪明的蟑螂吗?(从爬行路线考虑)AB解:如图为圆柱的侧面展开图,AC=6–1=5,BC=24×=12,由勾股定理得AB²=AC²+BC²=169,∴AB=13(m).BAC即最短路线AB为13m12例3:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?【分析】由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度是否小于CH.如图所示点D在离厂门中线0.8米处,且CD⊥AB,与地面交于H.在Rt△OCD中,由勾股定理得CH=0.6+2.3=2.9(米)>2.5(米).因此高度上有0.4米的余量,所以卡车能通过厂222210.80.6(CDOCOD米)解:如图所示点D在离厂门中线0.8米处,且CD⊥AB,则OC=1米,OD=0.8米1.在△ABC中,∠B=90°AB=c,BC=a,AC=b。⑴若a=9,b=15,则c=;⑵若a=6,c=8,则b=;⑶已知a:c=3:4,b=25,求c=____.2.现准备将一块形为直角三角形的绿地扩大,使其仍为直角三角形,两直角边同时扩大到原来的两倍,问斜边扩大到原来的多少倍?小结:要根据题目画出相应的图形,切记不能死记公式的固定形式课堂练习cabABC121020(2倍)作业:同步导学