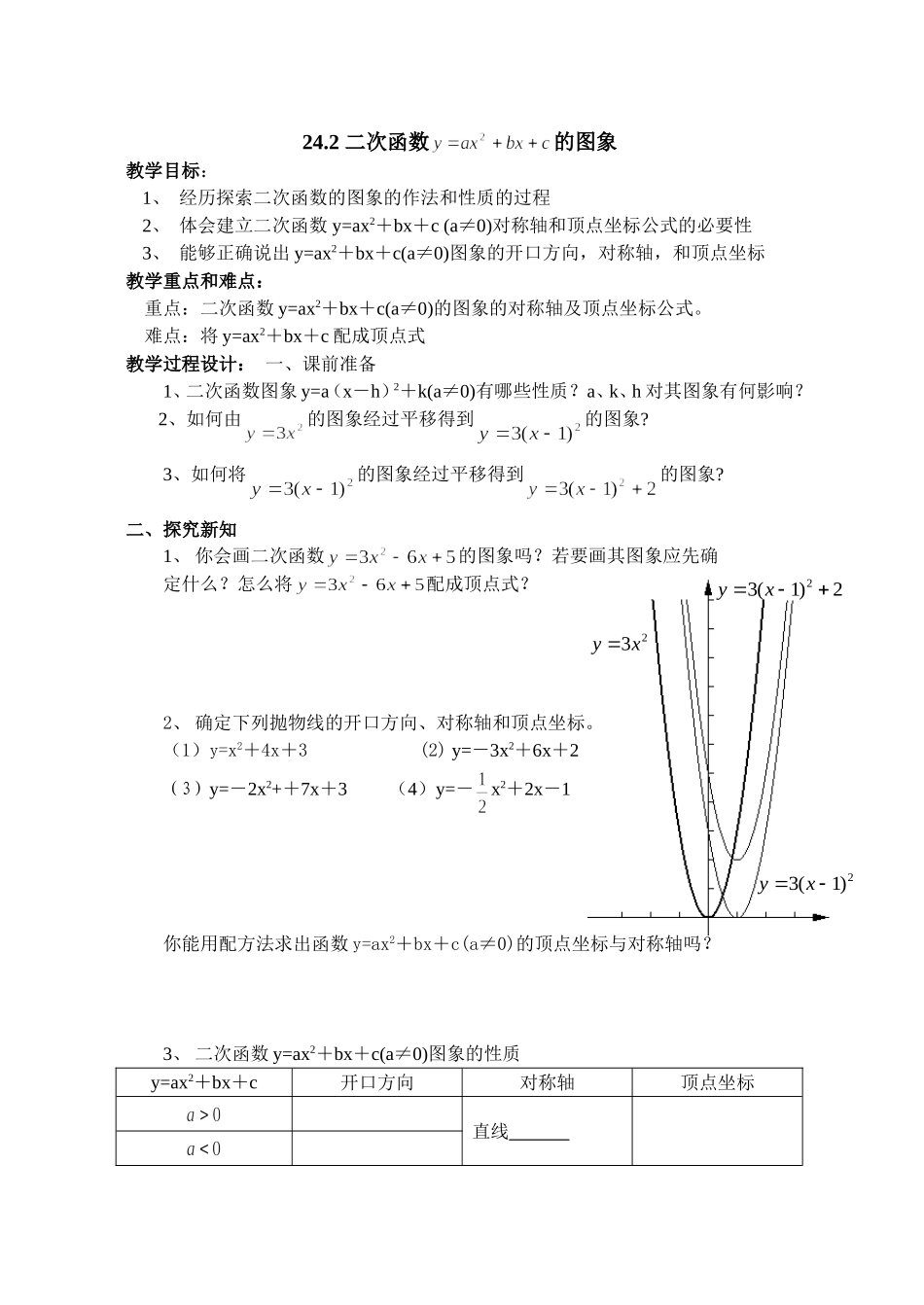
23xy2)1(3xy2)1(32xy24.2二次函数的图象教学目标:1、经历探索二次函数的图象的作法和性质的过程2、体会建立二次函数y=ax2+bx+c(a≠0)对称轴和顶点坐标公式的必要性3、能够正确说出y=ax2+bx+c(a≠0)图象的开口方向,对称轴,和顶点坐标教学重点和难点:重点:二次函数y=ax2+bx+c(a≠0)的图象的对称轴及顶点坐标公式。难点:将y=ax2+bx+c配成顶点式教学过程设计:一、课前准备1、二次函数图象y=a(x-h)2+k(a≠0)有哪些性质?a、k、h对其图象有何影响?2、如何由的图象经过平移得到的图象?3、如何将的图象经过平移得到的图象?二、探究新知1、你会画二次函数的图象吗?若要画其图象应先确定什么?怎么将配成顶点式?2、确定下列抛物线的开口方向、对称轴和顶点坐标。(1)y=x2+4x+3(2)y=-3x2+6x+2(3)y=-2x2++7x+3(4)y=-x2+2x-1你能用配方法求出函数y=ax2+bx+c(a≠0)的顶点坐标与对称轴吗?3、二次函数y=ax2+bx+c(a≠0)图象的性质y=ax2+bx+c开口方向对称轴顶点坐标直线三、学习体会:画形如y=ax2+bx+c(a≠0)的图象就注意什么?y=ax2+bx+c(a≠0)的对称轴是直线,顶点坐标是四、目标测试:1、求下列函数的最大值或最小值。(1)y=-x2-4x+2(2)y=x2-5x+(3)y=5x2+10(4)y=-2x2+8x2.下列说法正确的是()①函数开口向上②抛物线与y轴交于(0.3)③y=-3x2-6x+c的对称轴为x=2④将抛物线向左平移一给单位得到A1个、B2个、C3个、D4个、3.抛物线的开口方向,顶点的坐标是,当x<0时y随x增大而4、已知抛物线y=ax2+bx+c(a<0)经过点A(-2,0),O(0,0),B(-3,y),C(3,y),则y与y的大小关系是五、考点一角:二次函数的图象向左平移2个单位,再向上平移3个单位,得二次函数求b与c的值。