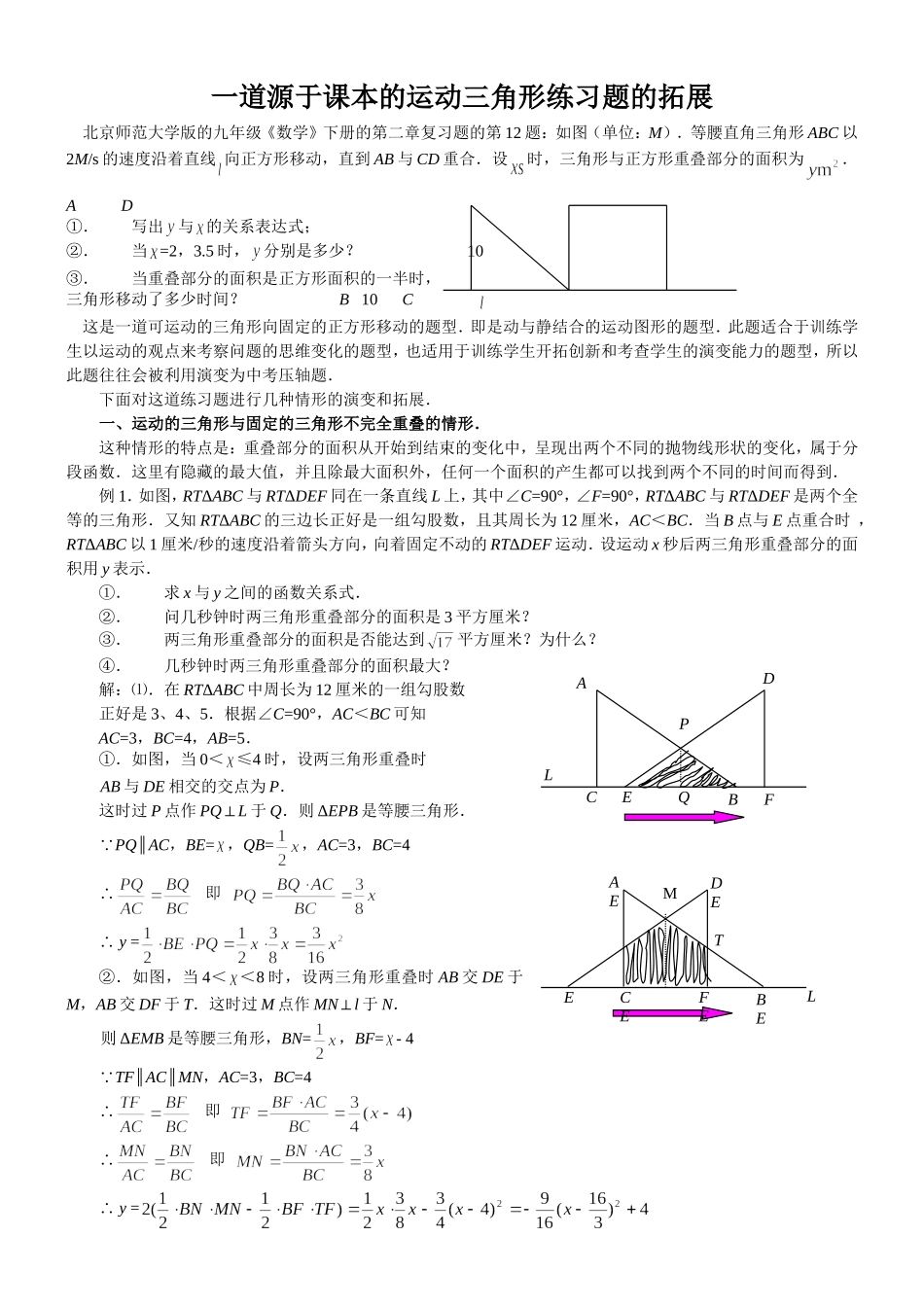
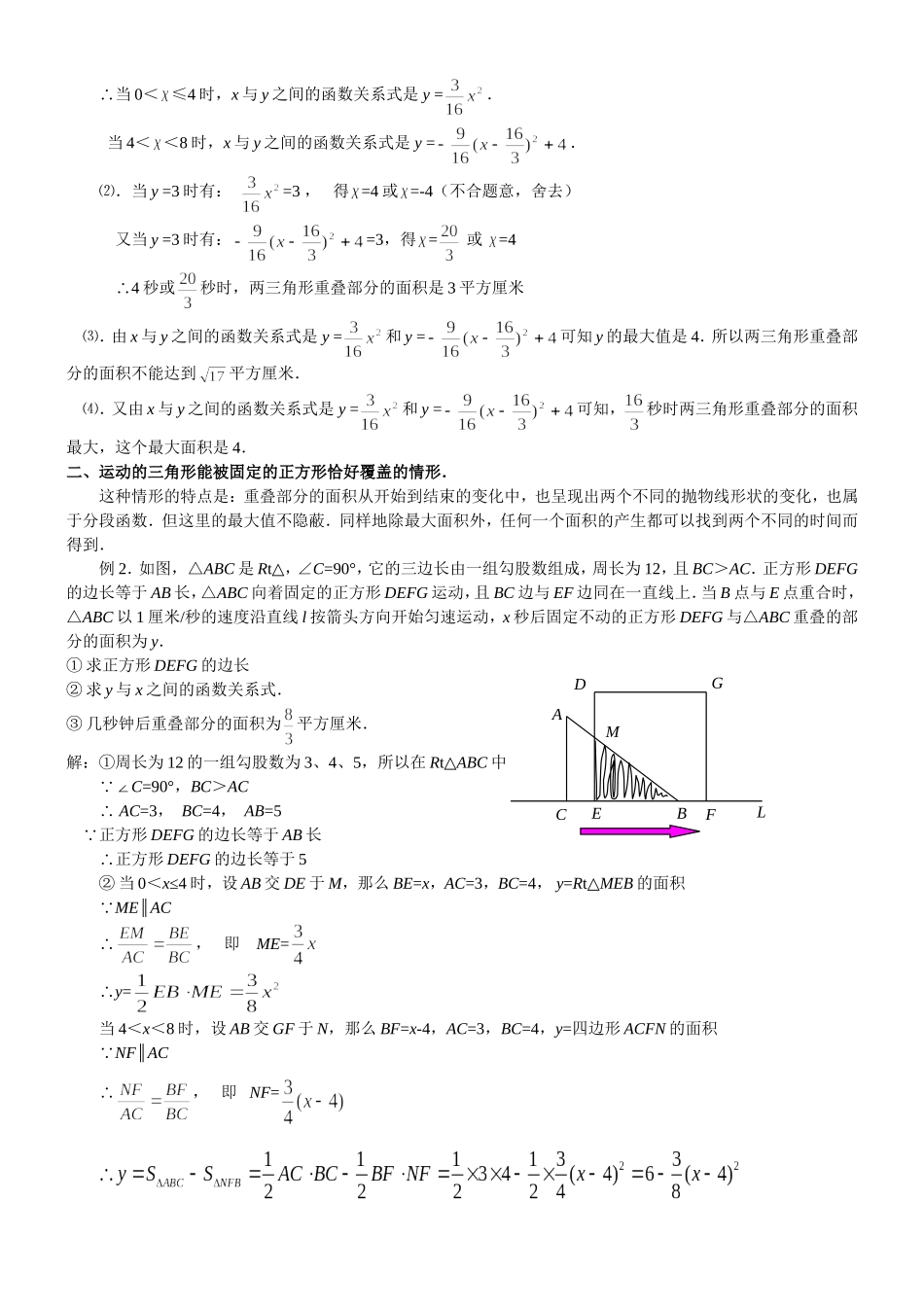
一道源于课本的运动三角形练习题的拓展北京师范大学版的九年级《数学》下册的第二章复习题的第12题:如图(单位:M).等腰直角三角形ABC以2M/s的速度沿着直线向正方形移动,直到AB与CD重合.设时,三角形与正方形重叠部分的面积为.AD①.写出与的关系表达式;②.当=2,3.5时,分别是多少?10③.当重叠部分的面积是正方形面积的一半时,三角形移动了多少时间?B10C这是一道可运动的三角形向固定的正方形移动的题型.即是动与静结合的运动图形的题型.此题适合于训练学生以运动的观点来考察问题的思维变化的题型,也适用于训练学生开拓创新和考查学生的演变能力的题型,所以此题往往会被利用演变为中考压轴题.下面对这道练习题进行几种情形的演变和拓展.一、运动的三角形与固定的三角形不完全重叠的情形.这种情形的特点是:重叠部分的面积从开始到结束的变化中,呈现出两个不同的抛物线形状的变化,属于分段函数.这里有隐藏的最大值,并且除最大面积外,任何一个面积的产生都可以找到两个不同的时间而得到.例1.如图,RTΔABC与RTΔDEF同在一条直线L上,其中∠C=90°,∠F=90°,RTΔABC与RTΔDEF是两个全等的三角形.又知RTΔABC的三边长正好是一组勾股数,且其周长为12厘米,AC<BC.当B点与E点重合时,RTΔABC以1厘米/秒的速度沿着箭头方向,向着固定不动的RTΔDEF运动.设运动x秒后两三角形重叠部分的面积用y表示.①.求x与y之间的函数关系式.②.问几秒钟时两三角形重叠部分的面积是3平方厘米?③.两三角形重叠部分的面积是否能达到平方厘米?为什么?④.几秒钟时两三角形重叠部分的面积最大?解:⑴.在RTΔABC中周长为12厘米的一组勾股数正好是3、4、5.根据∠C=90°,AC<BC可知AC=3,BC=4,AB=5.①.如图,当0<≤4时,设两三角形重叠时AB与DE相交的交点为P.这时过P点作PQ⊥L于Q.则ΔEPB是等腰三角形. PQ∥AC,BE=,QB=,AC=3,BC=4∴即∴y=②.如图,当4<<8时,设两三角形重叠时AB交DE于M,AB交DF于T.这时过M点作MN⊥l于N.则ΔEMB是等腰三角形,BN=,BF=-4 TF∥AC∥MN,AC=3,BC=4∴即∴即∴y=MTEFECEBELAEDEAPDFBQECL∴当0<≤4时,x与y之间的函数关系式是y=.当4<<8时,x与y之间的函数关系式是y=.⑵.当y=3时有:=3,得=4或=-4(不合题意,舍去)又当y=3时有:=3,得=或=44∴秒或秒时,两三角形重叠部分的面积是3平方厘米⑶.由x与y之间的函数关系式是y=和y=可知y的最大值是4.所以两三角形重叠部分的面积不能达到平方厘米.⑷.又由x与y之间的函数关系式是y=和y=可知,秒时两三角形重叠部分的面积最大,这个最大面积是4.二、运动的三角形能被固定的正方形恰好覆盖的情形.这种情形的特点是:重叠部分的面积从开始到结束的变化中,也呈现出两个不同的抛物线形状的变化,也属于分段函数.但这里的最大值不隐蔽.同样地除最大面积外,任何一个面积的产生都可以找到两个不同的时间而得到.例2.如图,△ABC是Rt△,∠C=90°,它的三边长由一组勾股数组成,周长为12,且BC>AC.正方形DEFG的边长等于AB长,△ABC向着固定的正方形DEFG运动,且BC边与EF边同在一直线上.当B点与E点重合时,△ABC以1厘米/秒的速度沿直线l按箭头方向开始匀速运动,x秒后固定不动的正方形DEFG与△ABC重叠的部分的面积为y.①求正方形DEFG的边长②求y与x之间的函数关系式.③几秒钟后重叠部分的面积为平方厘米.解:①周长为12的一组勾股数为3、4、5,所以在Rt△ABC中 ∠C=90°,BC>AC∴AC=3,BC=4,AB=5 正方形DEFG的边长等于AB长∴正方形DEFG的边长等于5②当0<x≤4时,设AB交DE于M,那么BE=x,AC=3,BC=4,y=Rt△MEB的面积 ME∥AC∴,即ME=∴y=当4<x<8时,设AB交GF于N,那么BF=x-4,AC=3,BC=4,y=四边形ACFN的面积 NF∥AC∴,即NF=LMDGFBECA③当y=,且y=时,得∴(不和题意,舍去)又当y=,且y=时,得=∴∴(不和题意,舍去)∴当秒或秒后重叠部分的面积为平方厘米.三、运动的三角形与固定的三角形恰好完全重叠的情形.这种情形的特点是:重叠部分的面积从开始到结束的变化中,也呈现出两个不同的抛物线形状的变化,也属于分段函数.但这里的最大值也不隐蔽...