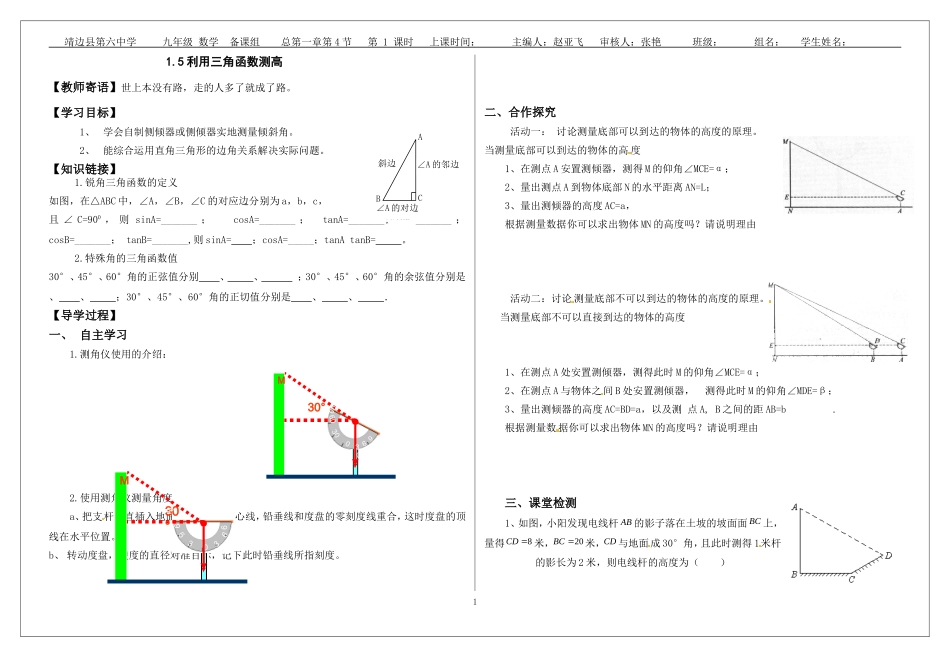
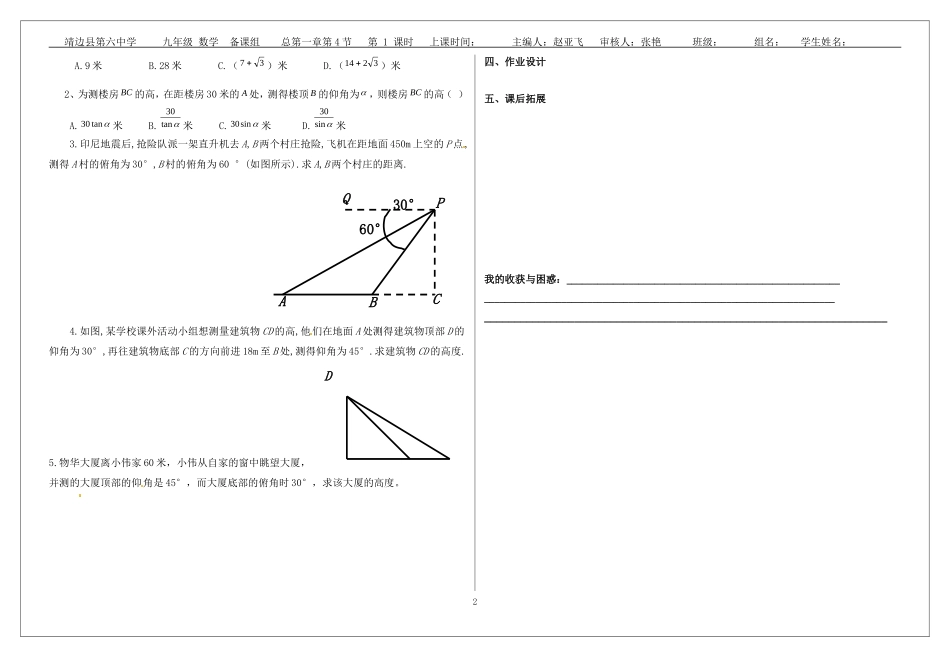
靖边县第六中学九年级数学备课组总第一章第4节第1课时上课时间:主编人:赵亚飞审核人:张艳班级:组名:学生姓名:1.5利用三角函数测高【教师寄语】世上本没有路,走的人多了就成了路。【学习目标】1、学会自制侧倾器或侧倾器实地测量倾斜角。2、能综合运用直角三角形的边角关系解决实际问题。【知识链接】1.锐角三角函数的定义如图,在△ABC中,∠A,∠B,∠C的对应边分别为a,b,c,且∠C=900,则sinA=_______;cosA=_______;tanA=_______;sinB=_______;cosB=_______;tanB=_______,则sinA=;cosA=_____;tanAtanB=。2.特殊角的三角函数值30°、45°、60°角的正弦值分别、、;30°、45°、60°角的余弦值分别是、、;30°、45°、60°角的正切值分别是、、.【导学过程】一、自主学习1.测角仪使用的介绍:2.使用测角仪测量角度的步骤:a、把支杆竖直插入地面,使支杆的中心线,铅垂线和度盘的零刻度线重合,这时度盘的顶线在水平位置。b、转动度盘,使度的直径对准目标,记下此时铅垂线所指刻度。二、合作探究活动一:讨论测量底部可以到达的物体的高度的原理。当测量底部可以到达的物体的高度1、在测点A安置测倾器,测得M的仰角∠MCE=α;2、量出测点A到物体底部N的水平距离AN=L;3、量出测倾器的高度AC=a,根据测量数据你可以求出物体MN的高度吗?请说明理由活动二:讨论测量底部不可以到达的物体的高度的原理。当测量底部不可以直接到达的物体的高度1、在测点A处安置测倾器,测得此时M的仰角∠MCE=α;2、在测点A与物体之间B处安置测倾器,测得此时M的仰角∠MDE=β;3、量出测倾器的高度AC=BD=a,以及测点A,B之间的距AB=b.根据测量数据你可以求出物体MN的高度吗?请说明理由三、课堂检测1、如图,小阳发现电线杆AB的影子落在土坡的坡面面BC上,量得8CD米,20BC米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为()1ABC∠A的对边∠A的邻边斜边M30°0303060609090PQ0303060609090M30°PQABCPQ30°60°D靖边县第六中学九年级数学备课组总第一章第4节第1课时上课时间:主编人:赵亚飞审核人:张艳班级:组名:学生姓名:A.9米B.28米C.(37)米D.(3214)米2、为测楼房BC的高,在距楼房30米的A处,测得楼顶B的仰角为,则楼房BC的高()A.tan30米B.tan30米C.sin30米D.sin30米3.印尼地震后,抢险队派一架直升机去A,B两个村庄抢险,飞机在距地面450m上空的P点,测得A村的俯角为30°,B村的俯角为60°(如图所示).求A,B两个村庄的距离.4.如图,某学校课外活动小组想测量建筑物CD的高,他们在地面A处测得建筑物顶部D的仰角为30°,再往建筑物底部C的方向前进18m至B处,测得仰角为45°.求建筑物CD的高度.5.物华大厦离小伟家60米,小伟从自家的窗中眺望大厦,并测的大厦顶部的仰角是45°,而大厦底部的俯角时30°,求该大厦的高度。四、作业设计五、课后拓展我的收获与困惑:____________________________________________________________________________________________________________________________________________________________________________________________2