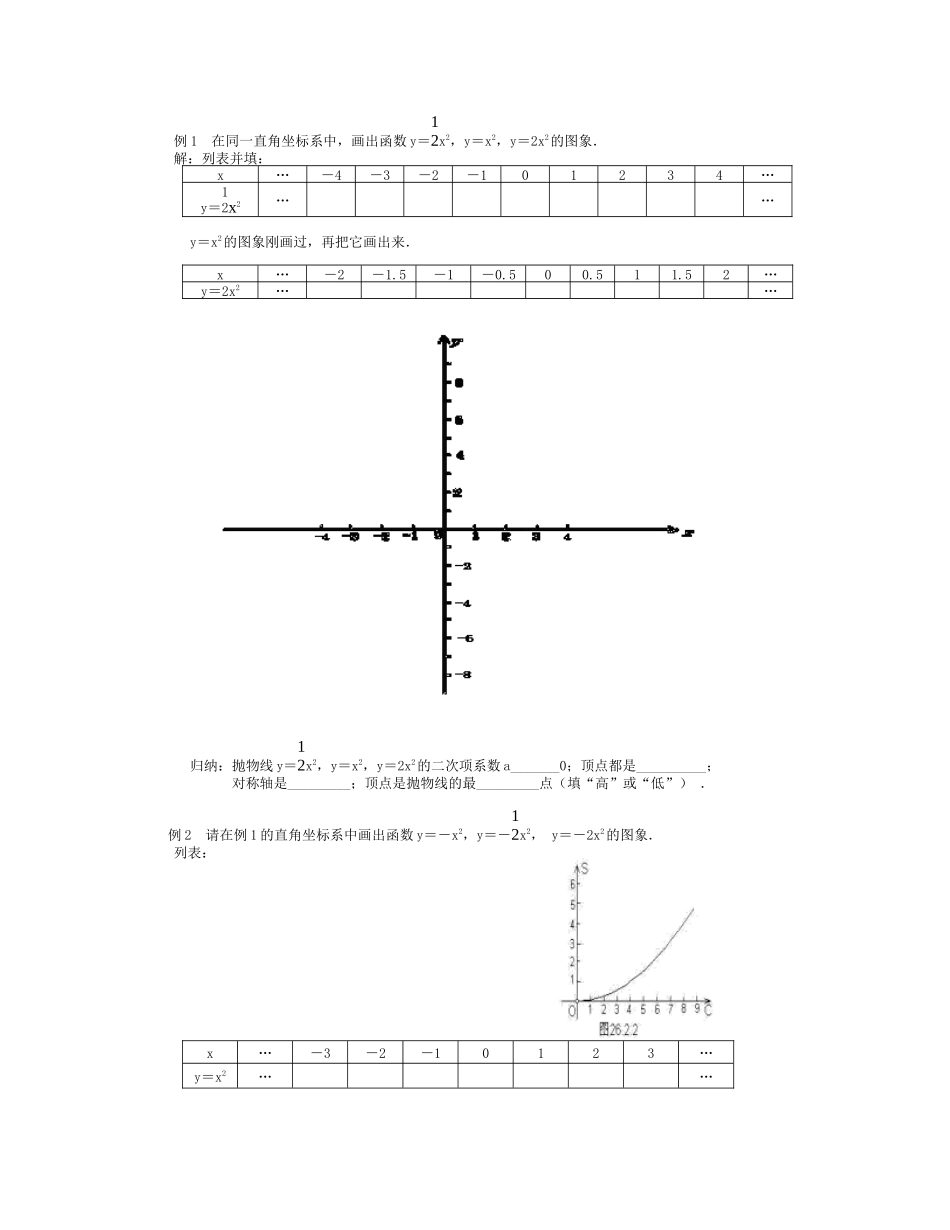
27.2二次函数的图象与性质1(第2课时)学习目标:1.知道二次函数的图象是一条抛物线;2.会画二次函数y=ax2的图象;3.掌握二次函数y=ax2的性质,并会灵活应用.学习重点:掌握二次函数y=ax2的性质,并会灵活应用.;学习难点:识图能力的培养一、知识回顾:1、二次函数的定义:一般地,形如y=叫做二次函数。2、二次函数的解析式:(1)一般形式:;(2)特殊形式3、如果函数是二次函数,那么m的值是()4、将函数y=(-2+3x)(5-x)化成一般形式是。5、画函数图象的步骤:(1);(2);(3)。前面学过,一次函数,反比例函数的图象分别是、,那么二次函数的图象是什么呢?它有什么特点?二、实践与探索三、探索新知:画二次函数y=x2的图象.【提示:画图象的一般步骤:①列表(取几组x、y的对应值;②描点(表中x、y的数值在坐标平面中描点(x,y);③连线(用平滑曲线).】列表:x…-3-2-10123…y=x2……描点,并连线由图象可得二次函数y=x2的性质:1.二次函数y=x2是一条曲线,把这条曲线叫做______________.2.二次函数y=x2中,二次函数a=_______,抛物线y=x2的图象开口__________.3.自变量x的取值范围是____________.4.观察图象,当两点的横坐标互为相反数时,函数y值相等,所描出的各对应点关于________对称,从而图象关于___________对称.5.抛物线y=x2与它的对称轴的交点(,)叫做抛物线y=x2的_________.因此,抛物线与对称轴的交点叫做抛物线的_____________.6.抛物线y=x2有____________点(填“最高”或“最低”).四、例题分析例1在同一直角坐标系中,画出函数y=12x2,y=x2,y=2x2的图象.解:列表并填:x…-4-3-2-101234…y=12x2……y=x2的图象刚画过,再把它画出来.x…-2-1.5-1-0.500.511.52…y=2x2……归纳:抛物线y=12x2,y=x2,y=2x2的二次项系数a_______0;顶点都是__________;对称轴是_________;顶点是抛物线的最_________点(填“高”或“低”).例2请在例1的直角坐标系中画出函数y=-x2,y=-12x2,y=-2x2的图象.列表:x…-3-2-10123…y=x2……x…-4-3-2-101234…y=-12x2……x…-4-3-2-101234…y=-2x2……归纳:抛物线y=-x2,y=-12x2,y=-2x2的二次项系数a______0,顶点都是________,对称轴是___________,顶点是抛物线的最________点(填“高”或“低”).五、理一理1.抛物线y=ax2的性质图象(草图)开口方向顶点对称轴有最高或最低点最值a>0当x=____时,y有最_______值,是______.a<0当x=____时,y有最_______值,是______.2.抛物线y=x2与y=-x2关于________对称,因此,抛物线y=ax2与y=-ax2关于_______对称,开口大小_______________.3.当a>0时,a越大,抛物线的开口越___________;当a<0时,|a|越大,抛物线的开口越_________;因此,|a|越大,抛物线的开口越________,反之,|a|越小,抛物线的开口越________.注意:在列表、描点时,要注意合理灵活地取值以及图形的对称性,因为图象是抛物线,因此,要用平滑曲线按自变量从小到大或从大到小的顺序连接.例2.已知是二次函数,且当时,y随x的增大而增大.(1)求k的值;(2)求顶点坐标和对称轴.试一试:已知函数是关于x的二次函数。(1)求m的值;(2)m为何值时,图象有最高点?求出最高点的坐标;此时,当x为何值时,y随x的增大而减小。例3.已知正方形周长为Ccm,面积为Scm2.(1)求S和C之间的函数关系式,并画出图象;(2)根据图象,求出S=1cm2时,正方形的周长;(3)根据图象,求出C取何值时,S≥4cm2.分析此题是二次函数实际应用问题,解这类问题时要注意自变量的取值范围;画图象时,自变量C的取值应在取值范围内.C2468……解(1)由题意,得.列表描点、连线,(2)根据图象得S=1cm2时,正方形的周长是cm.(3)根据图象得,当Ccm时,S≥4cm2.注意:(1)此图象原点处为空心点;(2)横轴、纵轴字母应为题中的字母C、S,不要习惯地写成x、y.(3)在自变量取值范围内,图象为抛物线的一部分.三、课堂练习:1、在同一直角坐标系中,画出下列函数的图象:(1);(2)。2、根据...