(东南大学高数课件)§§1.3.1-3函数极限.ppt3.pptVIP免费

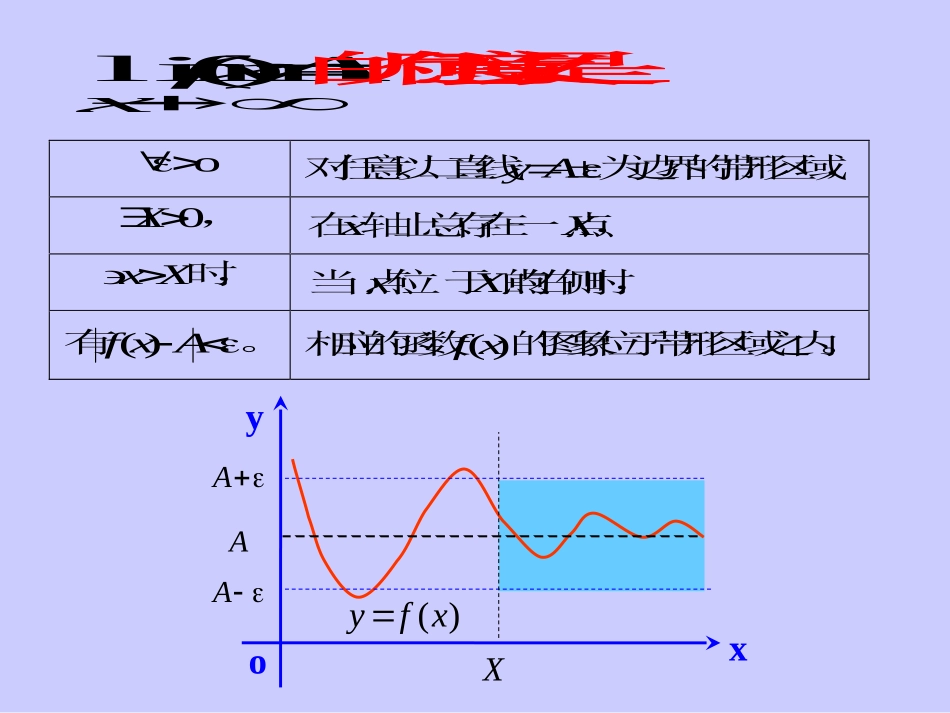
观察函数xxf1)(当x时的变化趋势。x是指x无限增大。xxx§1.3函数的极限xx1.3.1函数在无穷远处的极限xyoxxf1)(xo解：当x时，xxf1)(无限趋向于零。1．x时函数)(xf的极限定义定义：设)(xf在),a(内有定义，为A一定数。.)(lim.)(,,0,0AxfAxfXxXx恒有将Axfx)(lim与axnnlim列表对比如下：axnnlimAxfx)(lim函数nxy)(xfy定义域N),(a自变量的变化趋势nx函数值的变化趋势axnAxf)(.,,,0limaxNnNNaxnnn恒有.)(,,0,0)(limAxfXxXAxfx恒有Axfx)(lim的几何意义是：o对任意以二直线Ay为边界的带形区域，0X，轴在x上总存在X一点，Xx时，Xx位于点当点的右侧时，有Axf)(。相应的函数)(xf的图象位于带形区域之内。)(xfyAAAXxyo定义：设)(xf在),(a内有定义，A为一定数。Axfx)(lim.)(,,0,AxfXxXo恒有可以证明：AxfxfAxfxxx)(lim)(lim)(lim。2．x时函数)(xf的极限定义3．x时函数)(xf的极限定义定义：设)(xf当)0(aax时有定义，为A一定数。.)(,,0,0)(limAxfXxXAxfx恒有例1．证明111lim22xxx。证明：不妨设2x，0，要使11111122222xxxxx)11(12222xxx,2x只要2x，故取)2,2max(X，∴111lim22xxx。 0，0X，Xx时，恒有11122xx，例2．讨论函数xyarctan当x时的极限。yxo22xyarctan解：2arctanlimxx，2arctanlimxx， xxxxarctanlimarctanlim，∴xxarctanlim不存在。1.3.2函数在一点的极限一、xx时函数)(xf的极限例3．观察当x无限接近于1时，1)1(2)(2xxxf的变化趋势。当时无限接近于1x，)1(21)1(2)(2xxxxf无限接近于4。yxo41下面讨论如何用精确的定量化的语言来描述这种现象。当1x时，1241)1(24)(2xxxxf，任给存在使当恒有10120120110x1014)(xf10012001200110x10014)(xf10001200012000110x100014)(xf…………0210x4)(xf①定义中的xx0表明，当xx时)(xf有无极限与)(xf在点x有无定义无关。1．当xx时函数)(xf的“—”极限定义若o，0，xx0时，恒有Axf)(，则称常数A为函数)(xf当xx时的极限，记作Axfxx)(lim或)()(时当xxAxf。2．极限定义剖析②xx0表示点),(xNx落在内，Axf)(表示)(xf落在),(AN内。③定义中的定量地刻划了xx与的接近程度，定量地刻划了Axf与)(的接近程度。是正数，依赖于。但即使对于同一个，也不是唯一的。“”定义中两个不等式的关系是：Axf)(的根据是找是左式成立的条件xx0)(xfyo任意以直线Ay与Ay为边界的带形区域0总存在（以点x为心的）半径0当xx0时当点去心邻域的落在点xx),(xN之中恒有Axf)(相应的函数)(xfy的图形落在这个带形区域内。xyo3．Axfxx)(lim的几何意义),(xNxxxAyAy),(ANAAA例4．证明：（1）0sinlim0xx；（2）axaxcoscoslim。证明：（1）0，要使xxxsin0sin，只要x0，故取， 0，，00x时，恒有0sinx，∴0sinlim0xx。（2）0，要使axcoscos，即要使axaxaxaxax2122sin2sin2coscos，只要ax0，故取， 0，，ax0时，恒有axcoscos，∴axaxcoscoslim。特别地，有特别地，有.10coscoslim0xx可以证明：xxxx...