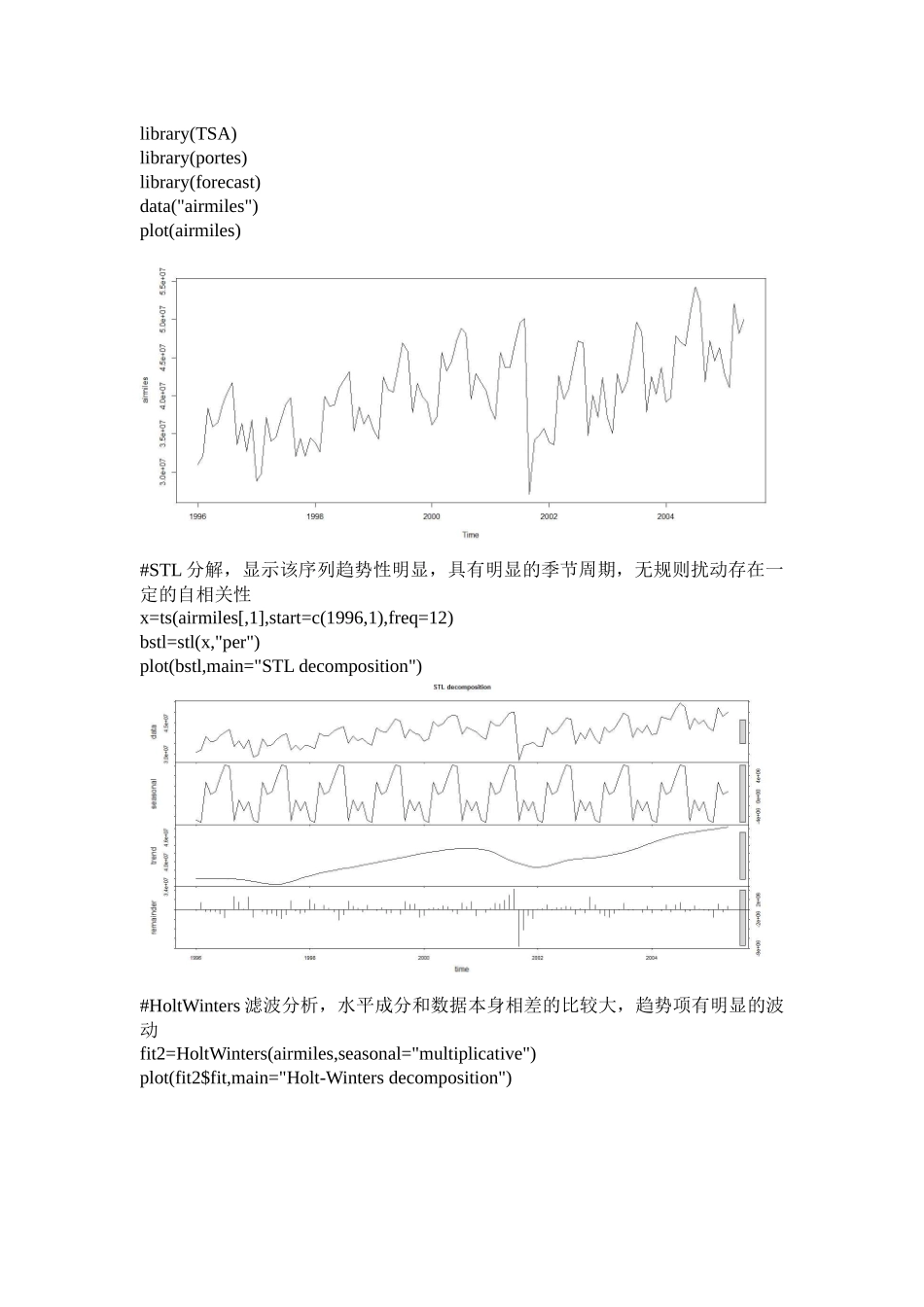
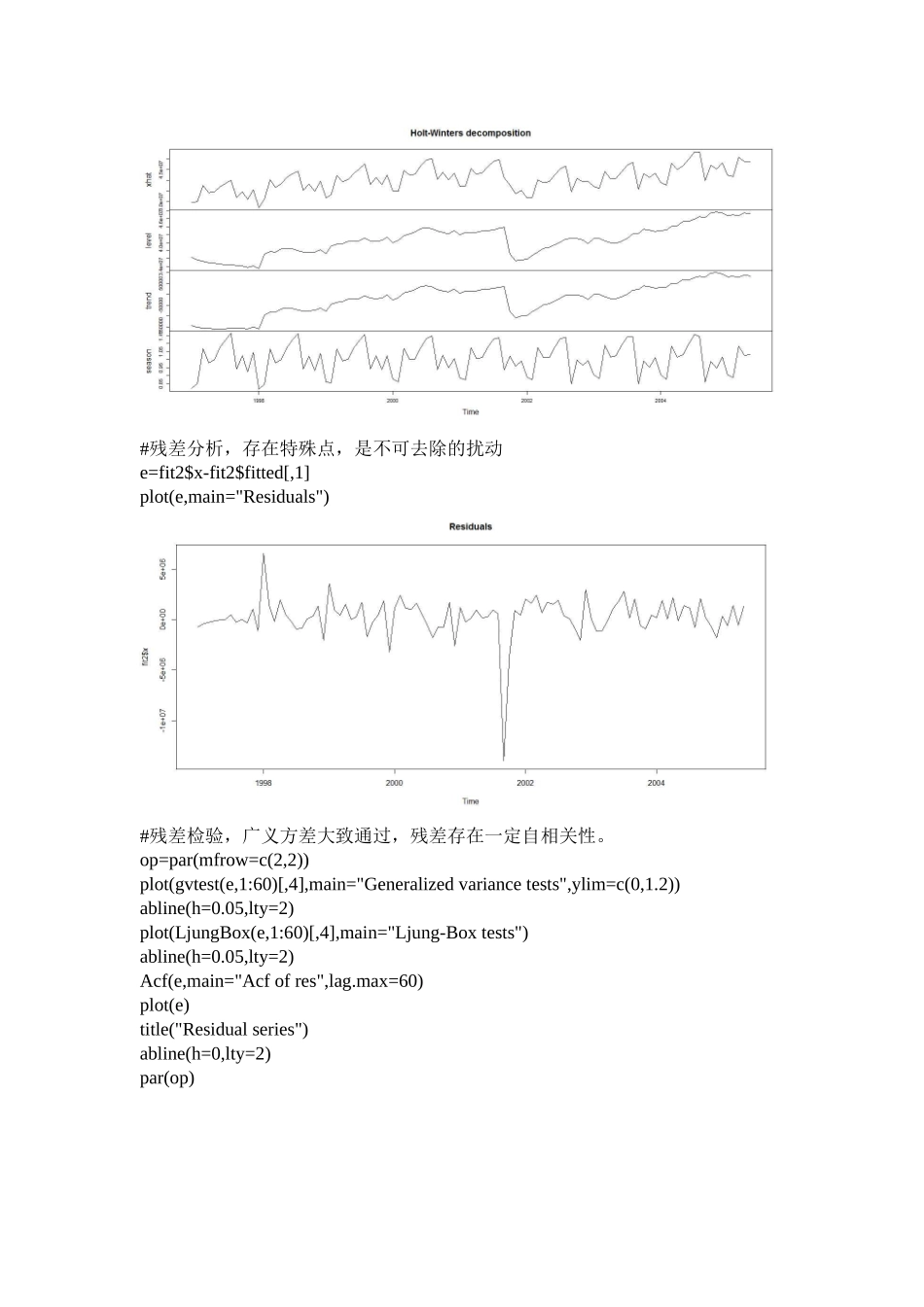
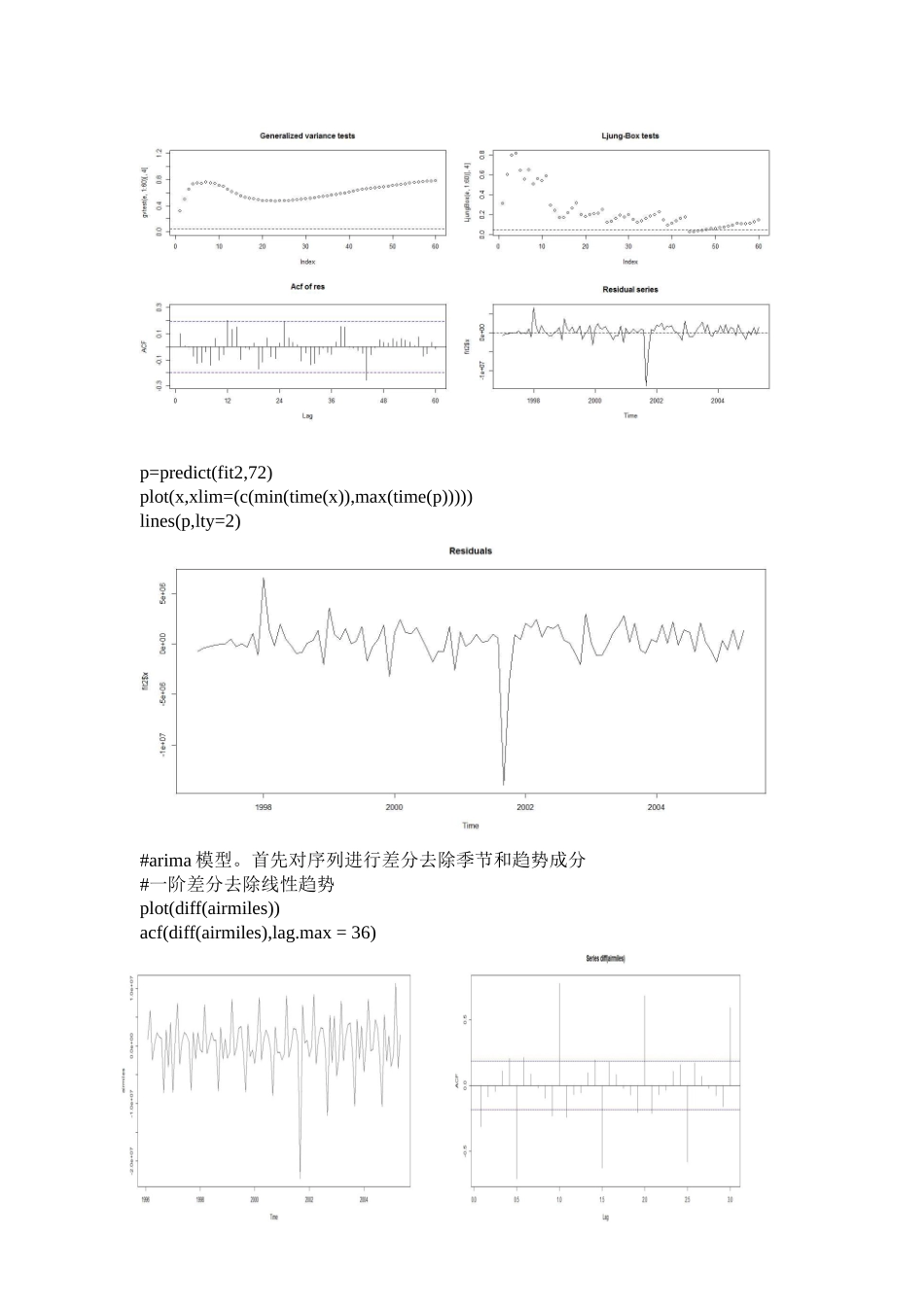
library(TSA)library(portes)library(forecast)data("airmiles")plot(airmiles)#STL分解,显示该序列趋势性明显,具有明显的季节周期,无规则扰动存在一定的自相关性x=ts(airmiles[,1],start=c(1996,1),freq=12)bstl=stl(x,"per")plot(bstl,main="STLdecomposition")#HoltWinters滤波分析,水平成分和数据本身相差的比较大,趋势项有明显的波动fit2=HoltWinters(airmiles,seasonal="multiplicative")plot(fit2$fit,main="Holt-Wintersdecomposition")#残差分析,存在特殊点,是不可去除的扰动e=fit2$x-fit2$fitted[,1]plot(e,main="Residuals")#残差检验,广义方差大致通过,残差存在一定自相关性。op=par(mfrow=c(2,2))plot(gvtest(e,1:60)[,4],main="Generalizedvariancetests",ylim=c(0,1.2))abline(h=0.05,lty=2)plot(LjungBox(e,1:60)[,4],main="Ljung-Boxtests")abline(h=0.05,lty=2)Acf(e,main="Acfofres",lag.max=60)plot(e)title("Residualseries")abline(h=0,lty=2)par(op)p=predict(fit2,72)plot(x,xlim=(c(min(time(x)),max(time(p)))))lines(p,lty=2)#arima模型。首先对序列进行差分去除季节和趋势成分#一阶差分去除线性趋势plot(diff(airmiles))acf(diff(airmiles),lag.max=36)#明显的相关性具有一定间隔,存在显著季节自相关性,再作季节差分plot(diff(diff(airmiles),lag=12))acf(diff(diff(airmiles),lag=12),lag.max=36)#残差检验结果,广义方差均检验通过,残差存在不可去除的扰动部分。fit1=arima(airmiles,order=c(0,1,1),seasonal=list(order=c(0,1,1),period=12))BIC(fit1)op=par(mfrow=c(2,2))plot(gvtest(fit1$res,1:60)[,4],main="Generalizedvariancetests",ylim=c(0,1.2))abline(h=0.05,lty=2)plot(LjungBox(fit1$res,1:60)[,4],main="Ljung-Boxtests")abline(h=0.05,lty=2)Acf(fit1$res,main="Acfofres",lag.max=60)plot(fit1$res)title("Residualseries")abline(h=0,lty=2)par(op)#带95%置信区间拟合,结果显示在置信水平内拟合的结果比较合理。Y=predict(fit2,n.ahead=12,prediction.interval=T)plot(fit2,Y)#arima预测,在置信水平内的波动并不是很大,结果较为合理。zA=forecast(fit1,h=24)plot(zA,ylim=c(min(x),max(x)),ylab="")#单位根检验,对arima(0,1,1)(0,1,1)[12]进行单位根检验,结果P值均小于0.01,因此可拒绝原假设,认为没有单位根,即差分之后为平稳序列。adf.test(diff(diff(airmiles),lag=12),alt="stationary")pp.test(diff(diff(airmiles),lag=12),alt="stationary")