Hertz理论VIP免费

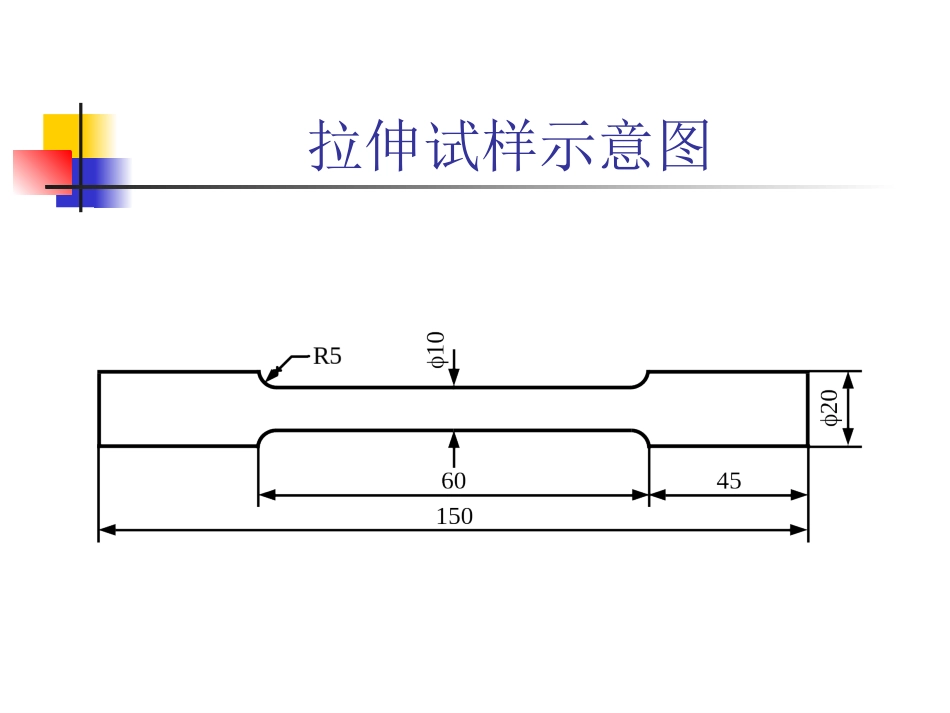
Hertz弹性接触理论1.弹性力学基础理论2.空间轴对称问题的基本微分方程3.空间轴对称问题4.弹性接触问题(Hertz弹性接触理论)5.一般接触问题弹性力学的应力与应变关系在弹性力学中假设物体是均匀、连续、和各向同性的，应力和应变的关系只决定于物体的物理性质，所以弹性力学与塑性力学的主要区别主要是应力和应变的关系定性。拉伸试样示意图PD3钢轨y=211860x-423.72030060090000.0050.010.0150.02应变ε/mm/mm应力σ/MPa物体的弹性变形曲线材料力学的虎克定律x=Ex式中E称为弹性模量，对于一种材料在一定温度下它是一个常数。应变关系在研究拉伸变形时沿受力的方向引起伸长，同时在垂直于力作用线的方向则引起缩短。根据实验得知，在弹性范围内，横向缩短和纵向相对伸长成正比，而缩短与伸长符号相反，故有：y=-x其中是弹性常数，称为波桑系数。应变与三向应力关系考虑应力x、y、z同时作用在x轴方向的应变，则有：x=[x-（y+z）]/E同理可以得到y轴和z轴方向的应变。剪应变与剪应力的关系同样的方法可以得出剪应变与剪应力的关系表达式：xy=xy/G式中G为剪切弹性模量。广义虎克定律将各向同性材料在空间应力状态时的应力与应变关系按上述方程式给出，即为广义虎克定律。由于进行三向均匀加力存在实验技术困难，广义虎克定律难与直接用实验来验证，但在长期的实践中已间接证明它的可靠性。2,空间轴对称问题的基本微分方程在工程中有不少问题，其几何形状和约束情况都是对称于z轴的。此时，用柱坐标表达则比较方便，所有各个分量都只是r和z的函数而与无关。这种问题称为空间轴对称问题。图１所示为一个微小弹性体，用相距dr的两个圆柱面，互成d的两个铅直面和相距dz的两个水平面组成。图中所有应力分量、应变分量和位移分量都将只是r和z的函数，不随变化。即以z轴为对称。图1注意到应力分量是（r，z）的函数，将各面上的应力分量写出，单位体积内的体积力在r、z方向的分量表示为fr、fz。根据此单元体在r方向的平衡方程：可以得：0rR022sin2sin22dzdrddrrfddzdrddzdrdrddrrdrddrrdzzdzrddzddrrdrrrzrzrzrrrr方程（１）因为d很小，所以可以认为式中的并略去高阶微量，并除以r·dr·d·dz，前式整理后可得：22sindd0rrzrrfrzr方程（１）同理可得z方向的平衡微分方程:0zrzzrzfrrz方程（２）进一步推导空间轴对称问题的几何变形方程:设u、w分别代表r及z轴方向的位移分量，则有关系式：rwzuzwrururzrrzr,0,,,方程（３）根据广义虎克定律，可得出物理方程：rzrzrzrzzzrzrrEGEEE12111令e为体积应变，即：zwruruezr前面各项式中共有１０个未知数，即：它们必需满足方程式（１，２，３）。当体积力Ｆ时，将方程（３）代入方程（１）中，便可得到位移表达的平衡方程式（５）。即为解空间轴对称问题的位移法的基本方程。rzzrrzzrwu,,,,,,,,,方程（５）22222222102110211zrrrwzeruure通过边界条件，求出满足方程式（５）的位移函数，然后代入到方程（２、３），即可求得应变及应力分量。3，空间轴对称问题设在弹性半空间体（即在一个方向界面，在其余各方向皆为无限大）的界面上，受垂直界面集中力Ｐ的作用，如图２所示。现用位移法求此时的位移及应力分量。图2求位移函数对空间轴对称问题，把Ｚ轴放在Ｐ力的作用线方向，将Ｐ力作用点作为坐标原点。当用位移法求解时,问题在于如何求出方程式(5)的解，并使之满足边界条件。通过解方程可以求得两组位移函数满足方程特解，...