地下水动力学 03-第三章 复习思考题答案VIP免费

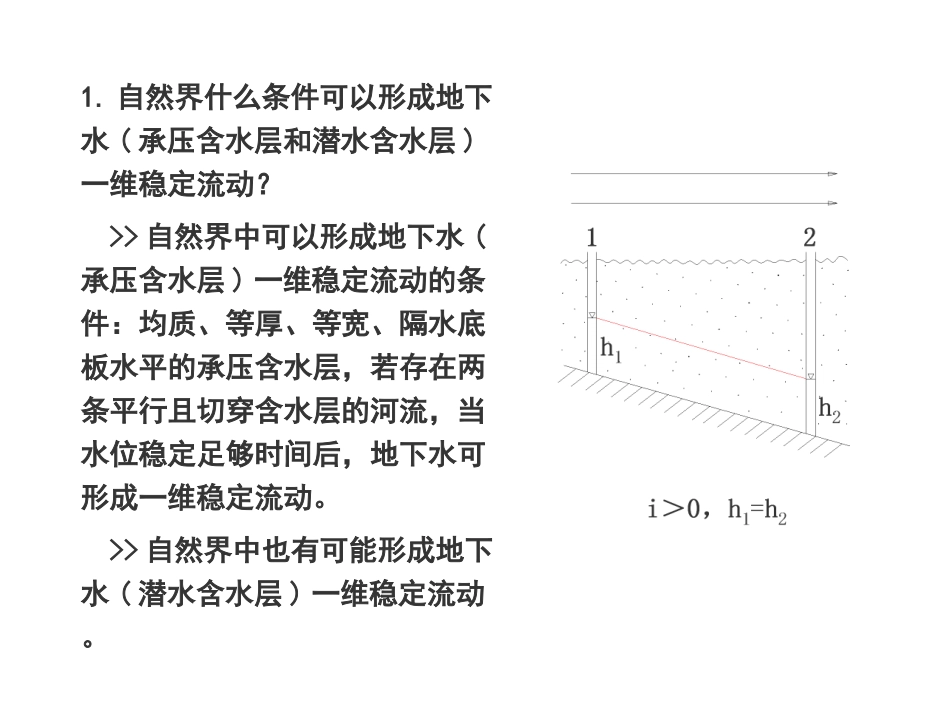
第三章复习思考题答案《地下水动力学》1.自然界什么条件可以形成地下水(承压含水层和潜水含水层)一维稳定流动？>>自然界中可以形成地下水(承压含水层)一维稳定流动的条件：均质、等厚、等宽、隔水底板水平的承压含水层，若存在两条平行且切穿含水层的河流，当水位稳定足够时间后，地下水可形成一维稳定流动。>>自然界中也有可能形成地下水(潜水含水层)一维稳定流动。2.自然界什么条件可以形成地下水(承压含水层和潜水含水层)剖面二维)(x，z)稳定流动？>>自然界中可以形成地下水(承压含水层)剖面二维稳定流动的条件：均质、等厚、等宽、隔水底板倾斜或弯曲的承压含水层，若存在两条平行且切穿含水层的河流，当水位稳定足够时间后，地下水可形成剖面二维稳定流动。>>自然界中可以形成地下水(潜水含水层)剖面二维稳定流动的条件：均质、等厚、等宽的潜水含水层，地下水可形成剖面二维稳定流动。3.什么条件下的稳定流水头线(或浸润曲线)与渗透系数无关？为什么？均质各向同性承压含水层中地下水稳定流的水头线(或浸润曲线)由及其边界条件确定。显然水头线方程与渗透系数无关。0222zHyHxH及其边界条件确定。显然，当W=0，即无蒸发、无入渗条件下，均质各向同性潜水含水层中地下水稳定流的水头线(或浸润曲线)与渗透系数无关；而当W≠0，即蒸发或入渗条件下，均质各向同性潜水含水层中地下水稳定流的水头线(或浸润曲线)与渗透系数有关。0WyhhyhxhhxhK均质各向同性潜水含水层中地下水稳定流的水头线(或浸润曲线)由可知沿流向将变大。所以水头线H为一上凸的曲线。4.试分析底坡i>0、i=0和i<0条件下均质潜水含水层二维流的浸润曲线出现的凹、凸和直线形状的可能性。对于底坡i=0和i<0条件下均质潜水含水层二维流，渗流宽度不变，而渗流厚度h沿流向变小。而根据渗流连续性原理，可知q=常量。那么，由裘布依微分方程xHKhqxH可知当h变小时，沿流向将变大，水头线H为一上凸且逐渐变弯的曲线；当h不变时，沿流向将不变，水头线H为一直线；当h变大时，沿流向将变小，水头线H为一下凹且逐渐变平的曲线。对于底坡i>0条件下均质潜水含水层二维流，渗流宽度不变，而渗流厚度h沿流向可能变小、不变或变大。根据渗流连续性原理，可知q=常量。那么，由裘布依微分方程xHKhqxHxHxH5.试建立图3-3-1所示的均质、等厚承压含水层，平面流线辐射形(平面二维流)稳定流的流量和水头线方程。图3-3-1承压含水层平面辐射流首先，建立如图所示的坐标系。根据偏微分形式的达西定律，任意断面的流量HxdxdHKAQBMA其中xlBBBB21112那么式1可变为dxdHxlBBBKMQ)(211对式2进行分离变量，并由断面1到断面2作积分，得2121101HHldHdxxlBBBKMQ式中：Q、K、M、B1、B2、l都是常数。那么，对上式进行积分后，得流量方程为)/ln())((121221BBlBBHHKMQ求水头线方程，可利用1-2断面和1-x断面分别写为Q1和Q2的流量方程，再根据水均衡原理，Q=Q1=Q2，则得到水头线方程BBBBBBBBxlHHHH121211211lnlnlnlnlhhWKl22022max邻6.如何得到欲修建水库水位的极限高度值hmax(不发生渗漏)？其大小与哪些水文地质条件有关？欲修建水库的水位的极限高度值hmax(不发生渗漏)由下式确定22max临hKWlh即1由式1可知，Hmax的大小与下述水文地质条件有关：>>K愈大，愈容易发生渗漏；>>渗流途径l越小，即水库与临河之间距越短，越容易发生渗漏；>>入渗补给量W愈小，愈容易渗漏；>>临河水位h临愈小，愈容易渗漏。7.在式3-1-22与3-1-23之间有一段文字，“若引进裘布依假定(实际上，此条件下并非处处满足裘布依假定)……”读者如何理解？何处不满足裘布依假定？>>由于裘布依假定是在渗流的垂直分流速远远小于水平分流速条件下，而忽略垂直分流速所获得的。因此，裘布依假定不能用在垂直分流速比较大而不能忽略的情况。>>在地下水分水岭处的铅直面十分接近流面或者就是流面，当然就不可能将其假定为等水头面。因此，地下水分水岭附近不满足裘布依假定。另外，在地下...