第4章 刚体的转动VIP免费

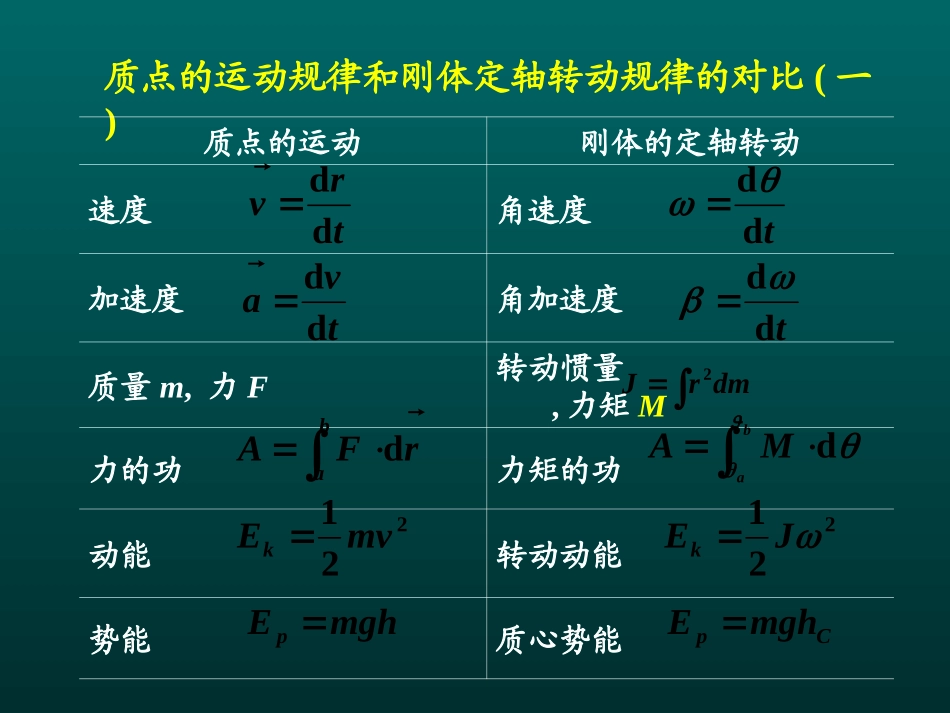
质点的运动规律和刚体定轴转动规律的对比(一)质点的运动刚体的定轴转动速度角速度加速度角加速度质量m,力F转动惯量,力矩M力的功力矩的功动能转动动能势能质心势能trvddtddtvaddtdd221mvEk221JEkbarFAdbaMAdmghEpCpmghEdmrJ2质点的运动规律和刚体定轴转动规律的对比(二)质点的运动刚体的定轴转动运动定律转动定律动量定理角动量定理动量守恒角动量守恒动能定理动能定理机械能守恒机械能守恒amFJM.constpkEE.constiiivm.constJ.constpkEE2022121JJW21222121mvmvW00ppdtFt1122JJdtM第四章刚体的转动部分习题分析与解答第四章刚体的转动部分习题分析与解答4－10如图(a)所示，圆盘的质量为m，半径为R．求：(1)以O为中心，将半径为R／2的部分挖去，剩余部分对OO轴的转动惯量；(2)剩余部分对O′O′轴(即通过圆盘边缘且平行于盘中心轴)的转动惯量．（1）解1转动惯量的定义，剩余部分的转动惯量为22/3222/2203215d2dπ2πdmRrrRmrrRmrmrJRRRR第四章刚体的转动部分习题分析与解答2121mRJ2222232122ππ21mRRRRmJ22103215mRJJJ解2整个圆盘对OO轴转动惯量为挖去的小圆盘对OO轴转动惯量剩余部分对OO轴的转动惯量为(2)由平行轴定理，剩余部分对O′O′轴的转动惯量为22222032392ππ3215mRRRRmmmRJ第四章刚体的转动部分习题分析与解答4-13如图所示，质量m1=16kg的实心圆柱体A，其半径为r=15cm，可以绕其固定水平轴转动，阻力忽略不计．一条轻的柔绳绕在圆柱体上，其另一端系一个质量为m2=8.0kg的物体B，求：（1）物体B由静止开始下降1.0s后的距离；（2）绳的张力．BAr2121rmJrFTamFgmFPTT222解(1)对实心圆柱体而言，由转动定律得对悬挂物体而言，依据牛顿定律，有（1）（2）第四章刚体的转动部分习题分析与解答αra21222mmgmam45.222121222mmgtmats且FＴ＝FＴ′.又由角量与线量之间的关系，得解上述方程组，可得物体下落的加速度在t＝1.0s时，B下落的距离为BArN2.3922121gmmmmagmFT(2)由式(2)可得绳中的张力为（3）第四章刚体的转动部分习题分析与解答分析：对平动的物体和转动的组合轮分别列出动力学方程，结合角加速度和线加速度之间的关系即可解得。解取分别对两物体及组合轮作受力分析如下图4-14质量为m1和m2的两物体A、B分别悬挂在如图所示的组合轮两端。设两轮的半径分别为R和r，两轮的转动惯量分别为J1和J2，轮与轴承间、绳索与轮间的摩擦力均略去不计，绳的质量也略去不计。试求两物体的加速度和强绳的张力。m2m1BABAFT2FT1FNPP1P2F’T2F’T1a1a2第四章刚体的转动部分习题分析与解答根据质点的牛顿定律和刚体的转动定律，有BAFT2FT1FNPP1P2F’T2F’T1a1a2)1(1111'11amFgmFPTT)2(22222'2amgmFPFTT)3()(2121JJrFRFTT)4(,2'21'1TTTTFFFF由角加速度和线加速度之间的关系，有)5(,21raRa第四章刚体的转动部分习题分析与解答解上述方程组，可得gRrmRmJJrmRma222121211grrmRmJJrmRma222121212gmrmRmJJRrmrmJJFT1222121222211gmrmRmJJRrmrmJJFT2222121121212第四章刚体的转动部分习题分析与解答分析：圆盘各部分的摩擦力的力臂不同，为此，可将圆盘分割成许多同心圆环，对环的摩擦力矩积分即可得总力矩。另由于摩擦力矩是恒力矩，由角动量定理可求得圆盘停止前所经历的时间。解（1）圆盘上半径为r、宽度为dr的同心圆环所受的摩擦力矩为4-17一半径为R，质量为m的匀质圆盘，以角速度ω绕其中心轴转动，现将它平放在一水平板上，盘与板表面的摩擦因数为μ。（1）求圆盘所受的摩擦力矩。（2）问经过多少时间后，圆盘转动才能停止？ωrdFdrkRmgdrrFdrMd)/2(22第四章刚体的转动部分习题分析与解答由于摩擦力矩是一恒力矩，圆盘的转动惯量J=mR2/2，由角动量定理可得圆盘停止的时间为gRMJt...