材料力学 第三章 扭转VIP免费

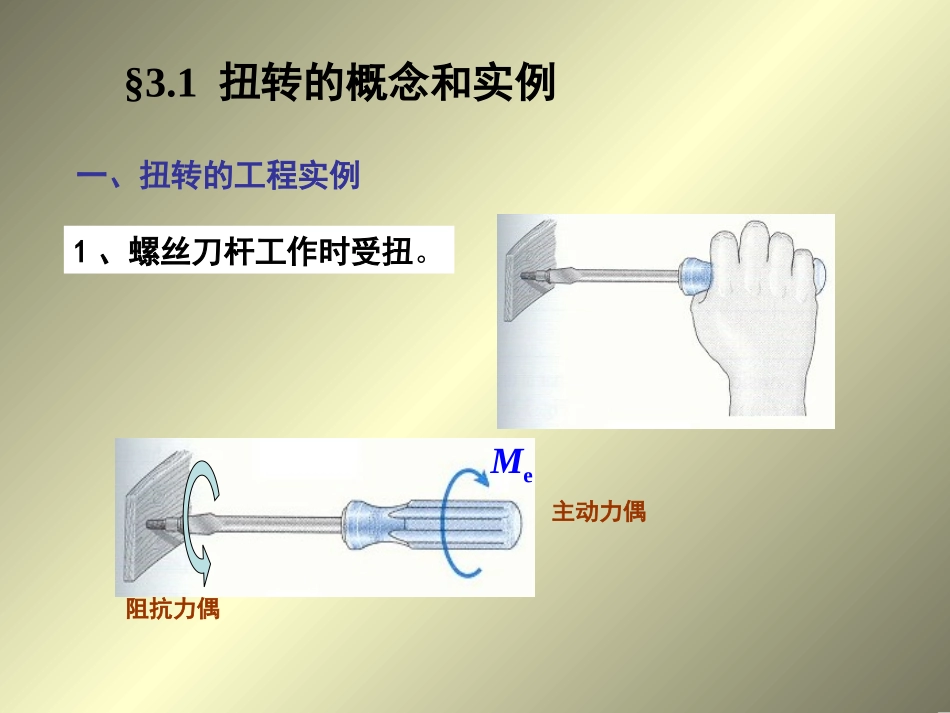
第三章扭转材料力学第三章扭转§3.1扭转的概念和实例§3.2外力偶矩的计算、扭转和扭矩图§3.3纯剪切§3.4圆轴扭转时的应力§3.5圆轴扭转时的变形§3.1扭转的概念和实例1、螺丝刀杆工作时受扭。Me主动力偶阻抗力偶一、扭转的工程实例2、汽车方向盘的转动轴工作时受扭。3、机器中的传动轴工作时受扭。受力特点：杆两端作用着大小相等、方向相反的力偶，且力偶作用面垂直于杆的轴线。变形特点：杆任意两截面绕轴线发生相对转动。主要发生扭转变形的杆——轴。AmMe主动力偶阻抗力偶em第三章扭转§3.1扭转的概念和实例§3.2外力偶矩的计算、扭转和扭矩图§3.3纯剪切§3.4圆轴扭转时的应力§3.5圆轴扭转时的变形§3.2外力偶矩的计算、扭转和扭矩图一、外力偶矩计算直接计算工程计算：按输入功率和转速计算电机每秒输入功：外力偶作功完成：)N.m(1000kPW602nMWekPkP已知轴转速－n转/分钟输出功率－Pk千瓦求：力偶矩Me圆轴受扭时其横截面上的内力偶矩称为扭矩，用符号T表示。eMT扭矩大小可利用截面法来确定。11TTMeMeAB11BMeAMe11xmm0,0mTmxT1、扭转杆件的内力（截面法）xmmmTTx取右段为研究对象：0,0TmmxmT取左段为研究对象：二、扭转杆件的内力——扭矩及扭矩图圆轴受扭时其横截面上的内力偶矩称为扭矩，用符号T表示。2、扭矩的符号规定：按右手螺旋法则判断。右手的四指代表扭矩的旋转方向，大拇指代表其矢量方向，若其矢量方向与截面的外法线方向相同，则扭矩规定为正值，反之为负值。T+T-3、内力图（扭矩图）表示构件各横截面扭矩沿轴线变化的图形。扭矩图作法：同轴力图：例1一传动轴如图，转速n=300r/min；主动轮输入的功率P1=500kW，三个从动轮输出的功率分别为：N2=150kW，N3=150kW，N4=200kW。试作轴的扭矩图。一、计算作用在各轮上的外力偶矩mkN9.15mN)3005001055.9(31MmkN78.4mN)1001501055.9(332MMmkN37.6mN)3002001055.9(34M解：M1M2M3M4ABCD二、分别计算各段的扭矩mkN78.421MTm9.56kN322MMTmkN37.643MT221133M1M2M3M4ABCDT111xM2AT2AM2BM322xT333DM4x扭矩图Tmax=9.56kN·m在BC段内M1M2M3M4ABCD4.789.566.37T图(kN·m)mkN78.41Tm9.56kN2TmkN37.63TmxMTAmlMA（m－轴单位长度内的扭力偶矩）例2试分析图示轴的扭矩)(xlmT表示扭矩沿杆件轴线变化的图线（T-x曲线）－扭矩图1、求约束反力2、截面法求扭矩D第三章扭转§3.1扭转的概念和实例§3.2外力偶矩的计算、扭转和扭矩图§3.3纯剪切§3.4圆轴扭转时的应力§3.5圆轴扭转时的变形§3.3纯剪切一、薄壁圆筒扭转时的剪应力0101rt,r0：为平均半径）(壁厚1、实验：2、变形规律：圆周线——形状、大小、间距不变，各圆周线只是绕轴线转动了一个角度。纵向线——倾斜了同一个角度，小方格变成了平行四边形。结论：,0000横截面上'可认为切应力沿壁厚均匀分布,且方向垂直于其半径方向。根据对称性可知切应力沿圆周均匀分布；,DtDt3、切应力的计算公式：2.2020200trtdrrdATAtrT202d薄壁圆筒横截面上的切应力计算式T:扭矩从受扭的薄壁圆筒表面处截取一微小的正六面体单元体——zyddzxddMeMexyzabOcddxdydz''0yF0zM自动满足0xFyzxxzydddddd存在'得二、切应力互等定理切应力互等定理单元体在其两对互相垂直的平面上只有切应力而无正应力的状态称为纯剪切应力状态。dabc''xyzabOcddxdydz''在相互垂直的两个面上，切应力总是成对出现，并且大小相等，方向同时指向或同时背离两个面的交线。二、剪应变、剪切胡克定律为扭转角lr0即lr0T——trT202lr0剪切虎克定律,pG)1(2EG在弹性范围内切应力与剪应变成正比关系。弹性模量、泊松比、剪应变模量之间的关系：第三章扭转§3.1扭转的概念和实例§3.2外力偶矩的计算、扭转和扭矩图§3.3纯剪切§3.4圆轴扭转时的应力§3.5圆轴扭...