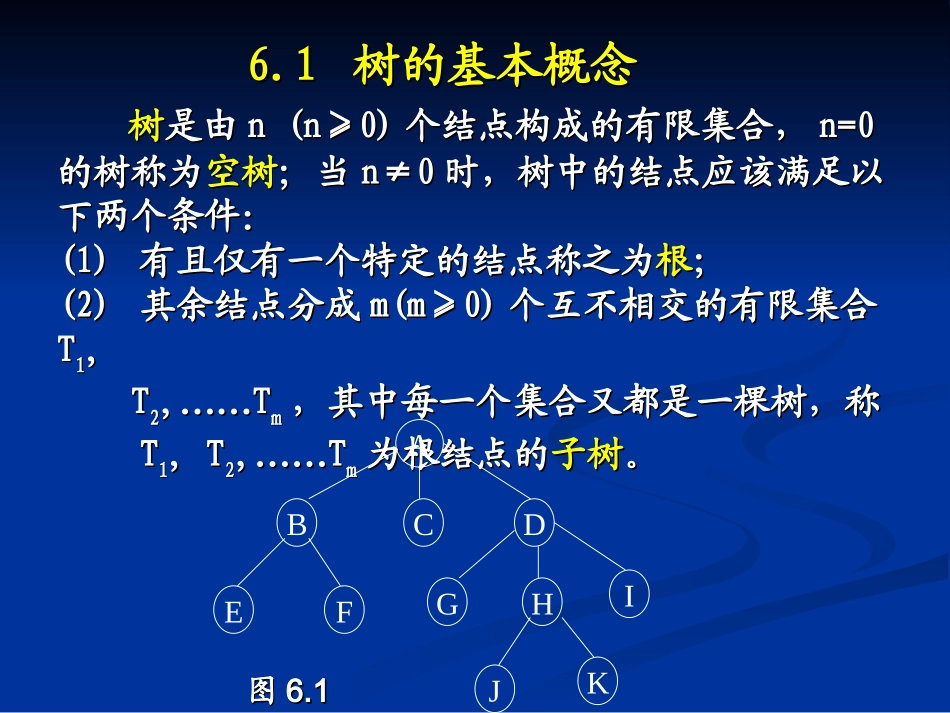
第第66章树型结构章树型结构树的基本概念树的基本概念树的遍历树的遍历树的线性表示树的线性表示树类的定义树类的定义树的存储结构树的存储结构6.16.1树的基本概念树的基本概念树树是由是由n(n≥0)n(n≥0)个结点构成的有限集合,个结点构成的有限集合,n=0n=0的树称为的树称为空树空树;当;当n≠0n≠0时,树中的结点应该满足以时,树中的结点应该满足以下两个条件:下两个条件:(1)(1)有且仅有一个特定的结点称之为有且仅有一个特定的结点称之为根根;;(2)(2)其余结点分成其余结点分成m(m≥0)m(m≥0)个互不相交的有限集合个互不相交的有限集合TT11,,TT22,,…………TTmm,其中每一个集合又都是一棵树,称,其中每一个集合又都是一棵树,称TT11,T,T22,,…………TTmm为根结点的为根结点的子树子树。。BDEFGAHIJKC图图6.16.1在树中采用线段连接两个相关联的结点,如在树中采用线段连接两个相关联的结点,如AA和和BB,,DD和和HH等。其中等。其中AA和和DD是上端结点,是上端结点,BB和和HH是下端是下端结点。称结点。称AA、、DD分别是分别是BB、、HH的的双亲双亲(或(或父母父母或或前件前件)),,BB和和HH分别为分别为AA和和DD的的子女子女(或(或孩子孩子或或后件后件)。显然)。显然,双亲和子女的关系是相对而言的。图,双亲和子女的关系是相对而言的。图6.16.1中,中,BB是是AA的子女,但又是的子女,但又是EE和和FF的双亲。由于的双亲。由于EE和和FF的双亲为同的双亲为同一结点,称一结点,称EE和和FF互为互为兄弟兄弟。在任何一棵树中,除根。在任何一棵树中,除根结点外,其它任何一个结点有且仅有一个双亲,有结点外,其它任何一个结点有且仅有一个双亲,有00个或多个子女,且它的子女恰巧为其子树的根结点。个或多个子女,且它的子女恰巧为其子树的根结点。我们将一结点拥有的子女数称为该我们将一结点拥有的子女数称为该结点的度结点的度,树中所,树中所有结点度的最大值称为有结点度的最大值称为树的度树的度。图。图6.16.1中,中,AA的度为的度为33,,BB的度为的度为22,而,而CC的度为的度为00,整棵树的度为,整棵树的度为33。称。称度为度为00的结点为的结点为终端结点终端结点或或叶子结点叶子结点,称度不为,称度不为00的的结点为非结点为非终端结点终端结点或或分支结点分支结点。显然,。显然,AA、、BB、、DD、、HH均为分支结点,而均为分支结点,而EE、、FF、、CC、、GG、、JJ、、KK、、II均为叶均为叶子结点。子结点。称树中连接两个结点的线段为称树中连接两个结点的线段为树枝树枝。在树中,。在树中,若从结点若从结点KKii开始沿着树枝自上而下能到达结点开始沿着树枝自上而下能到达结点KKjj,,则称从则称从KKii到到KKjj存在一条存在一条路径路径,路径的长度等于所经,路径的长度等于所经过的树枝的条数。在图过的树枝的条数。在图6.16.1中,从结点中,从结点AA到结点到结点JJ存在一条路径,路径的长度为存在一条路径,路径的长度为33;从;从DD到到KK也存在也存在一条路径,路径的长度为一条路径,路径的长度为22。仔细观察不难发现,。仔细观察不难发现,从树根到树中任何一个结点均存在一条路径。从树根到树中任何一个结点均存在一条路径。将从树根到某一结点将从树根到某一结点KKii的路径中的路径中KKii前所经过的前所经过的所有结点称为所有结点称为KKii的的祖先祖先;反之,以某结点;反之,以某结点KKii为根的为根的子树中的任何一个结点都称为子树中的任何一个结点都称为KKii的的子孙子孙。图。图6.16.1中中,,AA、、DD、、HH均为均为JJ和和KK的祖先,而的祖先,而GG、、HH、、II、、JJ和和KK均为均为DD的子孙。的子孙。树中树中结点的层次结点的层次:从树根开始定义,根结点为:从树根开始定义,根结点为第一层,根的子女结点构成第二层,依次类推,若第一层,根的子女结点构成第二层,依次类推,若某结点某结点KKjj位于第位于第ii层,则其子女就位于第层,则其子女就位于第i+1i+1层。层。称树中结点的最大层次数为树的称树中结点的最大层次数为树的深度深度或或高度高度。图。图6.16.1中,中,AA结点位于第一层,结点位于...