数据结构_树_PPT教程VIP免费

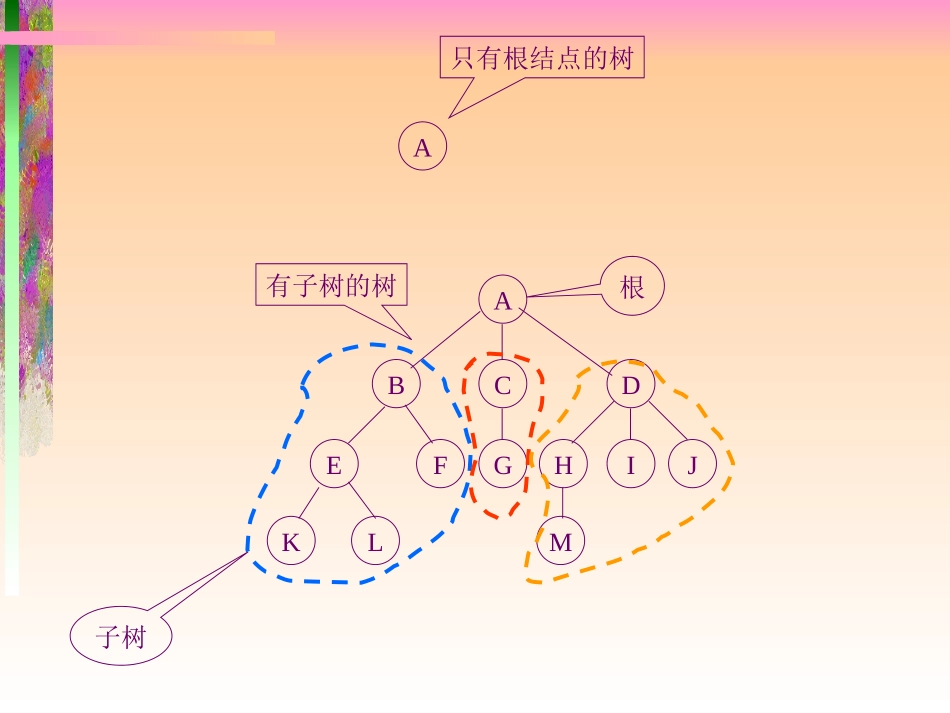
第五章树树是一类重要的非线性数据结构，是以分支关系定义的层次结构§5.1树的定义定义定义：树(tree)是n(n>0)个结点的有限集T，其中：有且仅有一个特定的结点，称为树的根(root)当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1,T2,……Tm，其中每一个集合本身又是一棵树，称为根的子树(subtree)特点：树中至少有一个结点——根树中各子树是互不相交的集合A只有根结点的树ABCDEFGHIJKLM有子树的树根子树基本术语结点(node)——表示树中的元素，包括数据项及若干指向其子树的分支结点的度(degree)——结点拥有的子树数叶子(leaf)——度为0的结点孩子(child)——结点子树的根称为该结点的孩子双亲(parents)——孩子结点的上层结点叫该结点的~兄弟(sibling)——同一双亲的孩子树的度——一棵树中最大的结点度数结点的层次(level)——从根结点算起，根为第一层，它的孩子为第二层……深度(depth)——树中结点的最大层次数森林(forest)——m(m0)棵互不相交的树的集合ABCDEFGHIJKLM结点A的度：3结点B的度：2结点M的度：0叶子：K，L，F，G，M，I，J结点A的孩子：B，C，D结点B的孩子：E，F结点I的双亲：D结点L的双亲：E结点B，C，D为兄弟结点K，L为兄弟树的度：3结点A的层次：1结点M的层次：4树的深度：4结点F，G为堂兄弟结点A是结点F，G的祖先§5.2二叉树定义定义：二叉树是n(n0)个结点的有限集，它或为空树(n=0)，或由一个根结点和两棵分别称为左子树和右子树的互不相交的二叉树构成特点每个结点至多有二棵子树(即不存在度大于2的结点)二叉树的子树有左、右之分，且其次序不能任意颠倒基本形态A只有根结点的二叉树空二叉树AB右子树为空AB左子树为空ABC左、右子树均非空二叉树性质性质1：)1(21iii个结点层上至多有在二叉树的第证明：用归纳法证明之i=1时，只有一个根结点，是对的假设对所有j(1j1，则其双亲是i/2(2)如果2i>n，则结点i无左孩子；如果2in，则其左孩子是2i(3)如果2i+1>n，则结点i无右孩子；如果2i+1n，则其右孩子是2i+1§5.3树的存储结构树的存储结构双亲表示法实现：定义结构数组存放树的结点，每个结点含两个域：数据域：存放结点本身信息双亲域：指示本结点的双亲结点在数组中位置特点：找双亲容易，找孩子难typedefstructnode{datatypedata;intparent;}JD;JDt[M];abcdefhgiacdefghib012235551096012345789dataparent0号单元不用或存结点个数如何找孩子结点孩子表示法多重链表：每个结点有多个指针域，分别指向其子树的根结点同构...