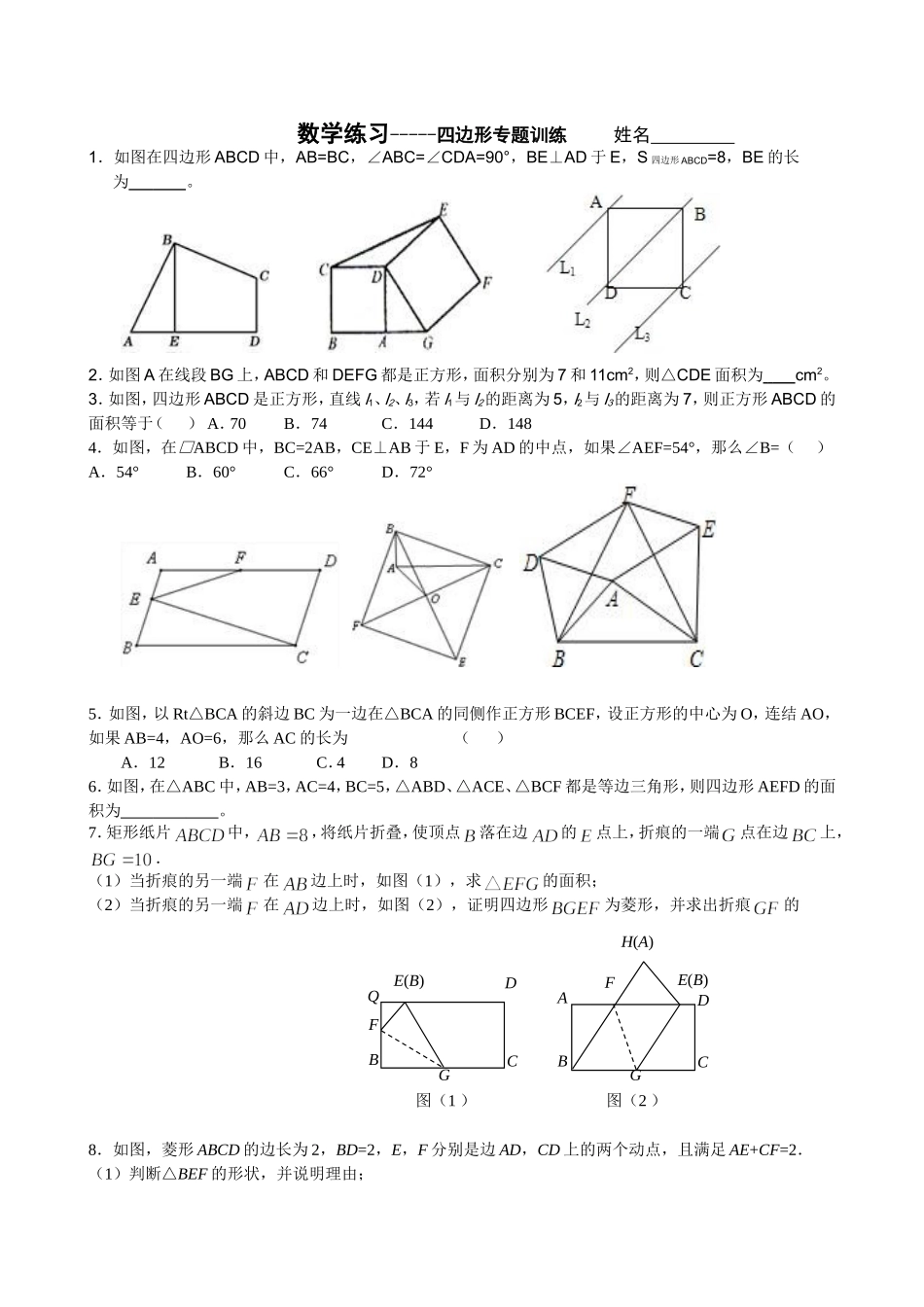
数学练习-----四边形专题训练姓名1.如图在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于E,S四边形ABCD=8,BE的长为。2.如图A在线段BG上,ABCD和DEFG都是正方形,面积分别为7和11cm2,则△CDE面积为cm2。3.如图,四边形ABCD是正方形,直线l1、l2、l3,若l1与l2的距离为5,l2与l3的距离为7,则正方形ABCD的面积等于()A.70B.74C.144D.1484.如图,在□ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,如果∠AEF=54°,那么∠B=()A.54°B.60°C.66°D.72°5.如图,以Rt△BCA的斜边BC为一边在△BCA的同侧作正方形BCEF,设正方形的中心为O,连结AO,如果AB=4,AO=6,那么AC的长为()A.12B.16C.4D.86.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为。7.矩形纸片中,,将纸片折叠,使顶点落在边的点上,折痕的一端点在边上,.(1)当折痕的另一端在边上时,如图(1),求的面积;(2)当折痕的另一端在边上时,如图(2),证明四边形为菱形,并求出折痕的8.如图,菱形ABCD的边长为2,BD=2,E,F分别是边AD,CD上的两个动点,且满足AE+CF=2.(1)判断△BEF的形状,并说明理由;QBFE(B)DCG图(1)图(2)GCDFABE(B)H(A)(2)设△BEF的面积为S,求S的取值范围.9.如图,△ABC中,BM平分∠ABC,AM⊥BM,垂足为M,点N为AC的中点,设AB=10,BC=6,求MN的长度.10.如图,△ABC的∠ABC的平分线BE与BC边的中线AD垂直且相等,已知BE=AD=4,求△ABC三边之长.11.如图,操作:把正方形CGEF的对角形CE放在正方形ABCD的边BC的延长线上(CG﹥BC),取线段AE的中点M.探索:(1)线段MD、MF的关系,并加以说明.ADFEBGMC(2)将正方形CGEF绕点C逆时针旋转45°,其他条件不变;如图探究:线段MD、MF的关系,并证明。12.如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,证明:①AF=FH,②∠HAE=45°,③BD=2FG,④△CEH的周长为定值,13.如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm。若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动.当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒。(1)直角梯形ABCD的面积为cm2;(2)当t=秒时,四边形PQCD成为平行四边形;BACEDFGMFEDABCHG第12题ABCDP(3)当t=秒时,AQ=DC;(4)是否存在t,使得P点在线段DC上且PQ⊥DC?若存在,求出此时t的值,若不存在,说明理由.14、如图1,正方形ABCD中,E、F分别是BC、CD上的点,∠EAF=450,则有结论EF=BE+DF成立;(1)如图2,在四边形ABCD中,AB=AD,∠B=∠D=900,E、F分别是BC、CD上的点,且∠EAF是∠BAD的一半,那么结论EF=BE+DF是否仍然成立?若成立请证明;若不成立,请说明理由;(2)若将(1)中的条件改为:在四边形ABCD中,AB=AD,∠B+∠D=1800,延长BC到E,延长CD到F,使得∠EAF仍然是∠BAD的一半,如图(3),则结论EF=BE+DF是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。15.如图①,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE.(不需要说明)(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF.则上面的结论①、②是否仍然成立?(请直接回答“成立”或“不成立”)(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出说明过程;若不成立,请说明理由.ABCDEF图(1)ABEFDC图(2)图(3)ABEFDC(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种?并写出说明过程.AAAABBBBCCCCDDDDEFEEEFFFGGGGMPQN图①图②图③图④