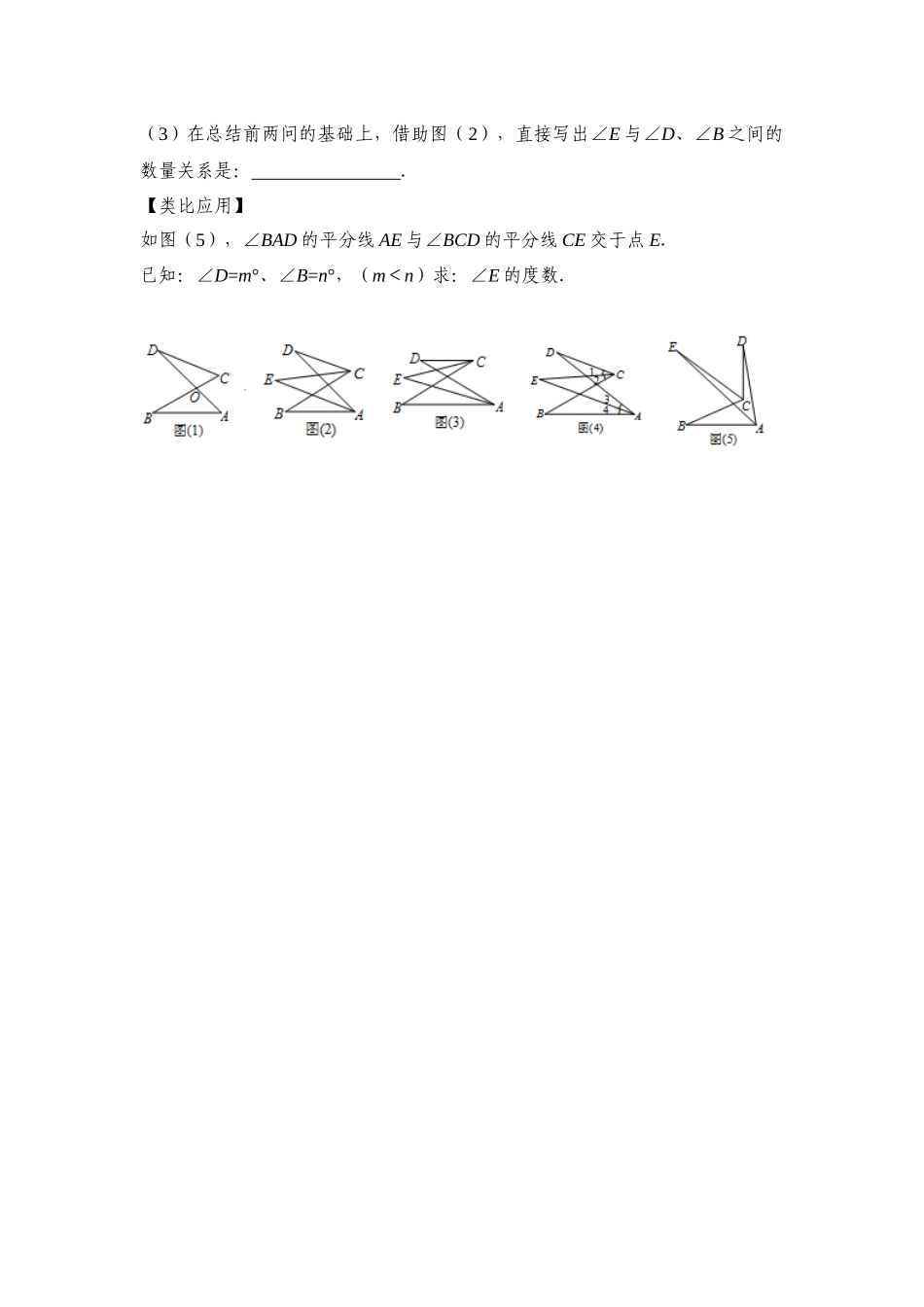
“8字形”在七年级几何中的妙用----好题推荐文昌湖区萌水中学王翠云13518634321原题章节:七年级下册第八章《平行线的有关证明》复习题原题位置:P64复习题联系拓广第18题原题:18.已知:如图,AM,CM分别平分∠BAD和∠BCD(1)如果∠B=32°,∠D=38°,求∠M的度数;(2)求证:∠M=(∠B+∠D)好题原因:题目本身难度不是很大,但对于七年级的学生来说解决这类综合试题,运用常规的解题方法难以解决,在解决本题时复习了三角形中出现的“8字形”特征学生迎刃而解,“8字形”特征在几何证明中作用很大,这道题就是应用“8字形”的特征来解决的好题,同时也注意了整体思想的利用。(1)解:根据三角形内角和定理∠B+∠BAM=∠M+∠BCM∠BAM-∠BCM=∠M-∠B同理,∠MAD-∠MCD=∠D-∠M∵AM、CM分别平分∠BAD和∠BCD∴∠BAM=∠MAD,∠BCM=∠MCD∴∠M-∠B=∠D-∠M∴∠M=(∠B+∠D)=(32°+38°)=35°(2)证明:根据三角形内角和定理∠B+∠BAM=∠M+∠BCM∠BAM-∠BCM=∠M-∠B同理,∠MAD-∠MCD=∠D-∠M∵AM、CM分别平分∠BAD和∠BCD∴∠BAM=∠MAD,∠BCM=∠MCD∴∠M-∠B=∠D-∠M∴∠M=(∠B+∠D)应用训练:如图(1),AD,BC交于O点,根据“三角形内角和是180°”,不难得出两个三角形中的角存在以下关系:①∠DOC=∠AOB;②∠D+∠C=∠A+∠B.【提出问题】分别作出∠BAD和∠BCD的平分线,两条角平分线交于点E,如图(2),∠E与∠D、∠B之间是否存在某种数量关系呢?【解决问题】为了解决上面的问题,我们先从几个特殊情况开始探究.已知∠BAD的平分线与∠BCD的平分线交于点E.(1)如图(3),若AB∥CD,∠D=30°,∠B=40°,则∠E=.(2)如图(4),若AB不平行CD,∠D=30°,∠B=50°,则∠E的度数是多少呢?小明是这样思考的,请你帮他完成推理过程:易证∠D+∠1=∠E+∠3,∠B+∠4=∠E+∠2,∴∠D+∠1+∠B+∠4=,∵CE、AE分别是∠BCD、∠BAD的平分线,∴∠1=∠2,∠3=∠4.∴2∠E=,又∵∠D=30°,∠B=50°,∴∠E=度.(3)在总结前两问的基础上,借助图(2),直接写出∠E与∠D、∠B之间的数量关系是:.【类比应用】如图(5),∠BAD的平分线AE与∠BCD的平分线CE交于点E.已知:∠D=m°、∠B=n°,(m<n)求:∠E的度数.